|
Učebný cieľ kapitoly
Po preštudovaní tejto kapitoly by ste mali zvládnuť základné pojmy
statiky:
- Hmotný bod, hmotné teleso, stupne voľnosti pohybu hmotného bodu a telesa v
rovine a priestore
- Sila a silové účinky
- Silová sústava, výslednica silovej sústavy, určovanie veľkosti a polohy
výslednice
- Rovnice ekvivalencie, statické podmienky rovnováhy
- Čo sú to väzby a väzbové reakcie, uvoľňovanie telies
1.1 DOKONALE TUHÉ TELESO
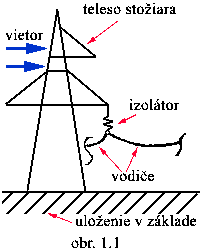
Z reálnej nepohyblivej konštrukcie (napr. stožiar vn
upevnený v betónovom základe a zaťažený vlastnou tiažou, tiažou
vodičov a vetrom) sa vytvorí mechanický model (statický systém):
Reálna konštrukcia
|
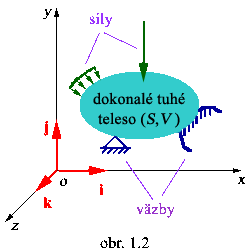
Statický systém
|
Statický systém ktorý je abstrakciou reálnej konštrukcie, nachádzajúci sa v okamžitom čase t v
statickej rovnováhe, obsahuje:
-
dokonale tuhé teleso (abstrakcia stožiara) s objemom V a povrchom S
-
vzťažný kartézsky súradnicový systém
O(x, y, z): i, j, k, sú bázové
jednotkové vektory
-
sily (dané pôsobením tiaže jednotlivých
konštrukčných prvkov, pôsobením vetra, elektormagnetického poľa, atď. ...)
-
väzby dané upevnením telesa
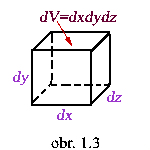 |
Hmotný bod -
časť hmotného telesa s elementárnym objemom dV [m3
] a elementárnym povrchom dS [m2] s
definovanou mernou hmotnosťou r
[kg/m3], obsahujúci veľké množstvo elementárnych
častíc hmoty. Častou geometrickou interpretáciou hmotného bodu
(jeho okolia) je elementárny hranol. Hmotné body budú označené
veľkými alebo malými písmenami, napr.: A, B, a, b, ...
|
V statike predpokladáme existenciu dokonale tuhého telesa, čo je len abstrakciou
reálneho telesa, ktoré je vždy poddajné. V niektorých prípadoch statiky možno
modelovať celé teleso jediným hmotným bodom - ťažiskom telesa,
kde je sústredená tiaž celého telesa.
1.2 SILA
Sila je mierou vzájomného mechanického pôsobenia telies
(alebo hmotných bodov).Označuje sa spravidla tučnými písmenami veľkej abecedy:
F, P, A, ...
Silové pôsobenie:
1. bez vzájomného styku

Na základe zákona akcie a reakcie sily vzájomného pôsobenia
sú rovnako veľké, t.j.
FAB= -FBA, resp.
FSZ = -FZS.
Akcia leží s reakciou na jednej nositeľke, je rovnako veľká, ale
opačne orientovaná. |
2. cez vzájomný styk
(bodový alebo plošný)
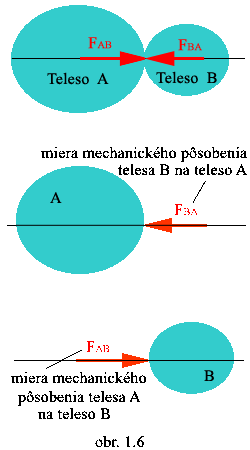 |
- vzájomné silové (mechanické) pôsobenie izolátora a
ramena stožiara
- vzájomné mechanické pôsobenie človeka a podložky
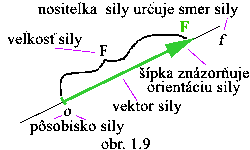 |
- Sila je fyzikálna veličina charakteru vektora.
- Má svoje pôsobisko, veľkosť, smer a orientáciu.
- Graficky sa znázorňuje ako orientovaná úsečka, ležiaca na
priamke - nositeľke sily. |
|
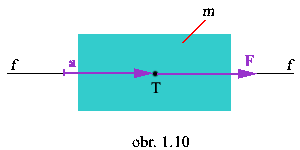
- Teleso s hmotnosťou m sa účinkom sily F pohybuje
zrýchlením a.
- Potom sila spôsobujúca tento pohyb
F = m.a
- Newtonov zákon sily.
- Vektory F a a sú rovnobežné, ležiace na spoločnej
priamke.
|
F = |F| = m|a| = ma
|
- je skalárna (na zmene vzťažného súradnicového systému
nezávislá) veličina,
je rovná absolútnej hodnote vektora sily.
- základná jednotka veľkosti sily: 1kg.(1m/s2)
= 1N (1 Newton)
- sila F = 1N udáva telesu o hmotnosti m = 1kg
zrýchlenie 1m/s2.
- odvodené jednotky: 1kN = 103N,
1MN = 106N
|
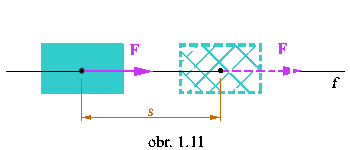 |
- práca vykonaná silou veľkosti F je: A = Fs
- jednotkou mechanickej práce je 1Joule,
značka [J]
- prácu rovnú 1J vykoná sila veľkosti 1N na
dráhe 1m (1J =1Nm)
- výkon sily je jej práca A vykonaná za určitý
čas t.
P = A/t[J/s]
- jednotkou výkonu je 1Watt, značka [W]
-výkon 1W predstavuje prácu 1J vykonanú za
čas 1 sekundy (1 J/s = 1 W) |
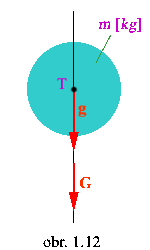
Na všetky hmotné telesá pôsobí graviračná sila úmerná jeho hmotnosti m[kg] a tiažovému
zrýchleniu g = 9,81 m/s2.
|
- veľkosť gravitačnej sily je G = m.g [N], a jej
výslednica, ktorá smeruje do
stredu Zeme (zvislý smer) pôsobí v ťažisku telesa
- na 1kg hmotnosti telesa pôsobí v gravitačnom poli Zeme gravitačná sila
G = 9,81 N. V technických výpočtoch sa táto sila často
zaokrúhľuje na
G = 10 N.
|
Silu ako vektor možno rozložiť na zložky v smere súradnicových osi:
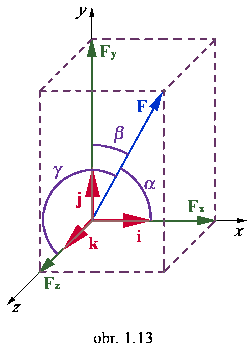
|
- v priestore:
Potom: F = Fx + Fy
+ Fz
= iFx + jFy +
kFz
Smerové uhly sily:
a,
b, g, pričom
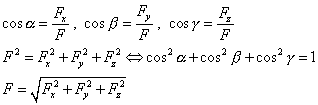
|
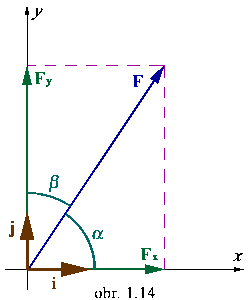
|
- v rovine:
F = Fx + Fy = i
Fx + jFy
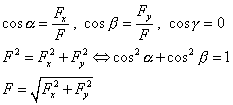
|
Pôsobenie sily na dokonalé tuhé hmotné teleso sa prejaví jeho
premiestnením, ktoré možno rozdeliť na posunutie a natočenie.
Ľubovoľná úsečka AB sa premiestni do polohy A´B´,
pričom AB = A´B´.
Sila teda má:
- posuvný účinok - PÚ
- otáčavý účinok - OÚ
PÚ - je charakterizovaný veľkosťou sily:
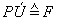 a je ku každému bodu telesa rovnaký.
a je ku každému bodu telesa rovnaký.
OÚ - je charakterizovaný momentom sily:
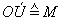
Moment sily je vektorom, a jeho veľkosť M = |M|
je k rôznym bodom telesa rôzna.
Úloha: Treba nájsť moment
sily F k bodu A.
- Platí: MA = rA × F
- rA je polohový vektor pôsobiska sily k počiatku
súradnicového systému uloženému do bodu A.
MA = rA F sin
a = F rA
sina = FpA [Nm]
- jednotkou veľkosti momentu je 1Nm (1 Newtonmeter).
- veľkosť momentu sily k bodu je rovná súčinu veľkosti sily a ramena sily.
- kolmá vzdialenosť nositeľky sily od bodu A - pA [m]
sa nazýva ramenom sily.
- Moment sily k bodu telesa je vektor, ktorého nositeľka je kolmá na rovinu tvorenej
nositeľkou sily a polohovým vektorom daného bodu.
- Jeho orientácia je daná jednotkovým vektorom e, pre
ktorého orientáciu platí pravidlo pravej ruky:
Moment sily je kladný, ak polohový vektor a sila tvoria
pravotočivý systém (proti pohybu hodinových ručičiek). V opačnom
prípade je moment sily k danému bodu záporný (v smere pohybu
hodinových ručičiek).
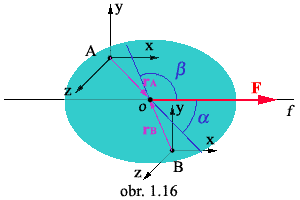
Úloha: Stanovte smer a orientáciu
momentu sily k bodom A a B.
|
|
Moment sily k bodu A:
- posunutím vektora rA
do bodu o dostaneme
pravotočivý systém dvoch vektorov.
- moment sily k bodu A je kladný.
|
Moment sily k bodu B:
- posunutím vektora rB do bodu o dostaneme
ľavotočivý systém dvoch vektorov.
- moment sily k bodu B je záporný.
|
|
- potom: MA = rA × F
= eA MA
- eA je jednotkový vektor kolmý na rovinu
tvorenú vektormi rA a F.
eA = |eA| = 1
- veľkosť momentu MA = + F rA
sina
- kladný moment má znamienko plus.
|
- potom: MB = rB × F
= eB MB
- eB je jednotkový vektor kolmý na rovinu
tvorenú vektormi rB a F.
eB = |eB| = 1
- veľkosť momentu MB = - F rB
sinb
- záporný moment má znamienko mínus.
|
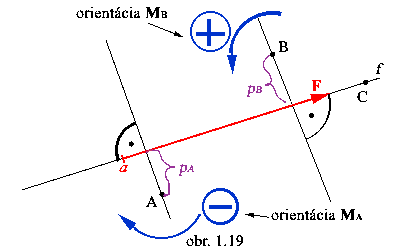
Úloha: Určite veľkosť a znamienko
momentov sily F k bodu A, B a C.
Všetky body i sila ležia v jednej rovine (bod C leží na
nositeľke sily).
|
|
Moment k bodu A
- točí na ramene sily pA
v smere pohybu hod.ručičiek
- je záporný
- teda MA = -pA F
|
Moment k bodu B
- je kladný
- teda MB = pB F
|
Moment k bodu C
- je rovný nule
t.j. MC = 0 lebo pC= 0
|
Všeobecne platí : Moment sily k ľubovolnému bodu
ležiacemu na jej nositeľke (tam leží aj pôsobisko sily) je rovný
nule (má nulový otáčavý účinok). K týmto bodom má len posuvný
účinok, ktorý je rovný veľkosti sily.
|
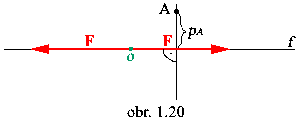
Úloha:
Určite silové účinky dvoch rovnako veľkých, ale opačne orientovaných síl ležiacich na
spoločnej nositeľke.
PÚ: F - F = 0
OÚ: FpA - FpA = 0 - platí k ľubovolnému bodu
|
|
Záver: Dve rovnako
veľké sily, ležiace na spoločnej nositeľke a opačne orientované majú
nulový silový účinok.
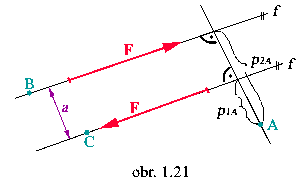
Úloha:
Určite silové účinky dvoch rovnako veľkých opačne orientovaných síl
ležiacich na paralelných nositeľkách, ktorých kolmá vzdialenosť je a.
PÚ: F - F = 0
OÚ: MA = Fp1A - Fp2A
= F(p1A - p2A ) = - Fa
MB = - Fa = MC = MA
|
|
Záver: Posuvný účinok je nulový,
otáčavý účinok je rovný súčinu veľkosti sily F a ich kolmej
vzdialenosti a, pričom je ku všetkým bodom telesa rovnaký.
Orientácia momentu je závislá na orientácii dvojice síl:
Transformáciou sily nahrádzame transformovanú
silu inou silou. Ak nová sila má rovnaké účinky ako sila pôvodná,
potom takáto náhrada je ekvivalentnou
transformáciou sily.
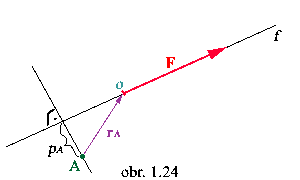
Úloha: Vykonajte ekvivalentnú
transformáciu sily F tak, aby jej nové pôsobisko bolo v
bode A.
|
Účinky sily F:
- posuvný účinok (PÚ): je rovný sile F
- otáčavý účinok (OÚ): MA = -p
AF
- PÚ aj OÚ majú byť zachované aj po transformácii
|
Transformáciu možno vykonať pripojením silovej
dvojice s nulovými účinkami do bodu A: dve rovnako veľké sily
F ležiace na spoločnej nositeľke, ale opačne orientované.
Čiže :
Posuvný účinok všetkých troch síl:
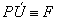
Otáčavý účinok všetkých troch síl:
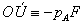
Záver : Silu F možno
ekvivalentne transformovať do iného pôsobiska tak, že do daného
bodu vložíme rovnakú silu F a moment MA =
rA × F.
Je to špeciálna transformácia sily. Posunutím sily po
jej nositeľke sa jej silové účinky nezmenia.
Dôkaz :
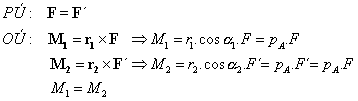
Posunutím sily po jej nositeľke sa jej statické účinky nemenia. Pozor:
deformačné účinky sily sa zmenia, t.j., deformácia poddajného telesa je závislá aj na
pôsobisku sily.
Sily delíme:
-
podľa charakteru
-
v o n k a j š i e (vyjadrujú
účinok okolitých telies a prostredia na vyšetrované teleso)
-
zaťažujúce (akcie)
-
väzbové reakcie (závislé od
akčných síl)
-
v n ú t o r n é (vyjadrujú
účinok jednej časti telesa na druhú. Vznikajú vo vnútri telesa ako odozva
na vonkajšie sily. Ak vnútorné sily prekročia určitú hranicu, dôjde k
veľkým deformáciám alebo ku porušeniu telesa.)
-
podľa rozloženia
-
s ú s t r e d e n é (sila
F[N] alebo moment sily M[Nm]), sú sústredené
do jedného bodu - pôsobiska
-
s p o j i t o r o z l o ž e n é
(V statike sa väčšinou ekvivalentne nahradzujú sústredenými silami.)
-
plošné (napr. tlak p [N/m2])
-
objemové (napr. vlastná tiaž
g [N/m3]
)
-
čiarové (napr. vlastná tiaž na jednotku
dĺžky telesa q [N/m].)
1.3 SILOVÁ SÚSTAVA
Dve a viacero síl pôsobiacich na teleso sa
nazýva silová sústava. Silové sústavy sa delia:
-
podľa rozloženia
-
c e n t r á l n e -nositeľky všetkých
síl sa pretínajú v jednom bode (obr. 1.29)
-
v š e o b e c n e
r o z p t ý l e n é
-nositeľky síl sa vzájomne pretínajú v rôznych bodoch
-
podľa rozmiestnenia v priestore
-
r o v i n n é
-nositeľky všetkých síl ležia v jednej rovine
-
p r i e s t o r o v é
-nositeľky síl sú rozložené v priestore
Priestorovú silovú sústavu možno transformovať na tri
rovinné sústavy ležiace v rovinách kartezského súradnicového systému.
Ďalej sa preto vo väčšine prípadov budeme zaoberať rovinnými sústavami
síl.
Silová sústava má posuvný a otáčavý účinok. Majme sily
F1, F2, ..., Fi
ležiace v jednej rovine.
Posuvný účinok SS
- je daný
súhrnom posuvných účinkov jednotlivých síl:
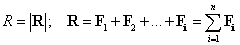
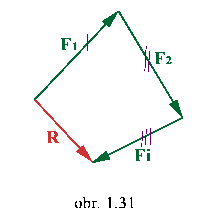
Výslednica všetkých síl R silový (vektorový)
obrazec uzatvára.
Platí:
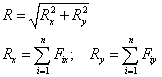
|
- veľkosť výslednice síl
- zložky výslednice síl
|
|
Otáčavý účinok SS
- k bodu telesa je daný súhrnom otáčavých účinkov (momentov)
jednotlivých síl:
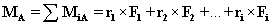
Vektor výsledného momentu rovinnej silovej sústavy je kolmý na rovinu
silovej sústavy a jeho veľkosť je k rôznym bodom rovinného telesa rôzna.
Jeho orientácia je závislá na orientácii a veľkosti momentov jednotlivých
síl.
Úloha: Vyjadrite posuvný a otáčavý
účinok síl F1 a F2 k bodu A.
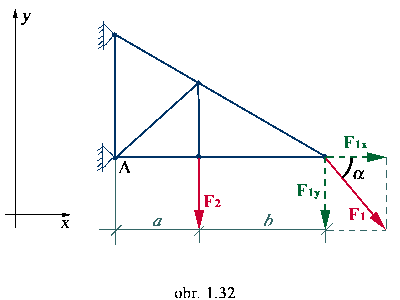
|
PÚ:- ku všetkým bodom ramena stožiara
je rovnaký
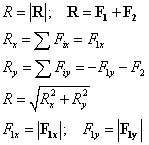
OÚ:
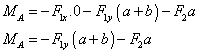
|
Treba ekvivalentne transformovať silovú sústavu F1,
F2,...,Fi do bodu A. Postupnou transformáciou
jednotlivých síl a ich momentov do bodu A a ich následným vektorovým súčtom dostaneme
výslednú silu R a výsledný moment MA.
Výslednicu silovej sústavy dostaneme ekvivalentnou transformáciou
všetkých síl do bodu, ku ktorému má silová sústava nulový otáčavý účinok. Silovú sústavu teda
nahradíme len jednou silou - výslednicou silovej sústavy
R. Pri hľadaní výslednice SS treba určiť jej
veľkosť, smer i orientáciu ako aj jej
pôsobisko. Slúžia nám na to rovnice
ekvivalencie, ktoré možno slovne vyjadriť aj takto:
Posuvný a otáčavý účinok SS k ľubovolnému bodu A musí byť rovnaký ako je
posuvný a otáčavý účinok výslednice R k
tomu istému bodu.
Vektorový tvar rovníc ekvivalencie:
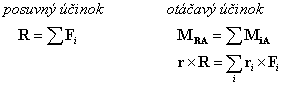
Skalárny tvar rovníc ekvivalencie:
priestorová SS
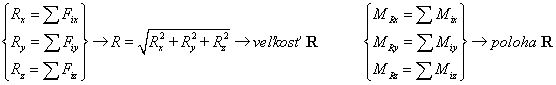
rovinná SS

Silová sústava je v statickej rovnováhe, ak jej posuvný a otáčavý účinok
je rovný nule. Takáto sústava síl sa nazýva rovnovážna silová
sústava. Ak na teleso (hmotný bod) pôsobí rovnovážna silová sústava, teleso
(hmotný bod) sa nachádza v statickej rovnováhe. Statickú rovnováhu možno popísať
statickými podmienkami rovnováhy, ktoré sú vyjadrením
nulovosti posuvného a otáčavého účinku silovej sústavy so silami F1,
F2, ..., Fi. Poznáme ich vektorový a skalárny tvar:
Vektorové rovnice rovnováhy SS:
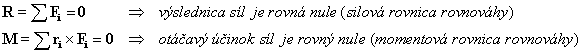
Skalárne (zložkové) rovnice rovnováhy SS:
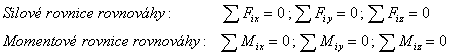
Rovnovážna priestorová silová sústava musí spĺňať súčasne
tri silové a tri momentové podmienky rovnováhy ku zvolenému SS. V silových rovniciach
rovnováhy sa sčítavajú zložky síl Fi v smere súradnicovej osi x, resp. y, resp. z.
V momentových rovniciach rovnováhy sa sčítavajú zložky momentov síl točiacich okolo
súradnicových osí x, resp. y , resp. z.
Ak silová sústava spĺňa statické podmienky k jednému
(ľubovolne zvolenému) súradnicovému systému, potom ich spĺňa ku všetkým ostatným
súradnicovým systémom.
Rovnovážna rovinná silová sústava musí spĺňať tri statické
podmienky rovnováhy:
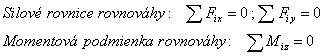
Rovnováha dvoch síl:
Dve sily sú v statickej rovnováhe, keď sú rovnako veľké, ležia na spoločnej
nositeľke a sú opačne orientované.
Rovnováha troch a viacerých síl centrálnej SS:
Centrálna silová sústava je v rovnováhe, keď jej výslednica je rovná
nule (nutnou i postačujúcou podmienkou je splnenie silových rovníc rovnováhy).
Rovnováha troch a viacerých síl všeobecne rozptýlenej SS:
Všeobecne rozptýlená rovnovážna silová sústava musí spĺňať všetky
silové i momentové podmienky rovnováhy.
Nulovosť výslednice je len nutnou
podmienkou statickej rovnováhy všeobecnej silovej sústavy. Typickým príkladom nerovnovážnej
silovej sústavy s nulovou výslednicou sú dve rovnako veľké, opačne orientované sily, ležiace
na paralelných nositeľkách (silová dvojica). Táto silová dvojica nespĺňa momentové podmienky
rovnováhy. V priebehu ďalších kapitol budeme používať pri hľadaní rovnovážnych stavov takmer
výlučne statické podmienky rovnováhy v skalárnom tvare.
1.4 VÄZBY
Objekty (telesa, hmotné body) sa spájajú navzájom
väzbami. V týchto väzbách vznikajú sily a momenty síl -
väzbové reakcie. Ak mechanickú sústavu (sústavu telies, bodov) tvorí niekoľko
objektov, potom sú medzi nimi tzv. vnútorné väzby, a reakcie
v nich sú vnútorné reakcie. Väzby, ktorými sa upevňuje sústava k
nepohyblivému telesu - tzv. rámu, sú
vonkajšie väzby, a reakcie v nich sú vonkajšie väzbové
reakcie.
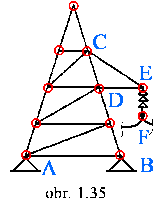
|
| Napr.: |
- V bodoch A a B sú väzby vonkajšie (pripevnenie stožiara o
betónový základ)
- V bodoch C, D, E, F, ... sú väzby vnútorné (medzi vodičmi a
izolátorom, izolátorom a ramenom stožiara, medzi prútmi prútovej
konštrukcie stožiara)
|
|
V smere väzbovej reakcie sa odoberá objektu možnosť pohybu (posuv, resp.
natočenie). Ak väzba odoberá možnosť pohybu len na jednu stranu, hovoríme o
jednostrannej väzbe. Ak sa odoberá v danom smere možnosť pohybu
na obidve strany, ide o väzbu dvojstrannú.
Jednostranná väzba
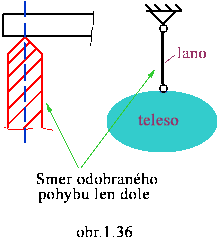
|
Dvojstranná väzba
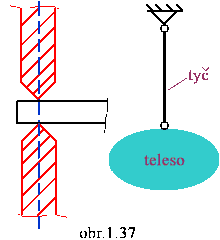
|
Veľkosť a orientácia väzbových reakcií závisí od akcií - vonkajšej
silovej sústavy. Väzbové reakcie sa vo väzbách usporiadajú tak, že spolu s akciami
tvoria rovnovážnu silovú sústavu. Veľkosť a orientáciu väzbových reakcií možno u
tzv. staticky určitých uloženiach určiť zo statických podmienok rovnováhy. Problematikou
väzieb a väzbových reakcií sa podrobnejšie zaoberá Kapitola 2 tejto učebnice.
|

 Výučba
Mechaniky
Výučba
Mechaniky