|
Učebný cieľ kapitoly
Po preštudovaní tejto kapitoly by ste mali vedieť:
- Ako je jednoznačne určená poloha hmotného bodu a telesa v rovine, resp. v
priestore
- Koľko stupňov voľnosti má hmotný bod a teleso v rovine, resp. v priestore
- Čo je to statická určitosť resp. neurčitosť uloženia a ako sa vypočíta
- Ako sa uvoľňujú väzby, ich náhrada väzbovými reakciami
- Ako možno vypočítať vonkajšie väzbové reakcie
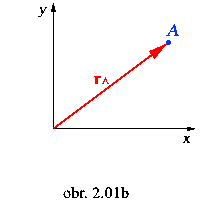
Poloha hmotného bodu v rovine i v priestore je jednojednoznačne určená
jeho polohovým vektorom vzhľadom na vzťažný súradnicový systém.
Priestor
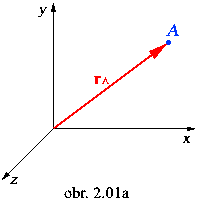 |
Rovina
 |
Poloha telesa v priestore je jednojednoznačne určená polohovými vektormi
jeho ľubovolných troch bodov neležiacich na jednej priamke.
Poloha telesa v rovine je jednojednoznačne určená polohovými vektormi jeho
ľubovolných dvoch bodov ležiacich v danej rovine.
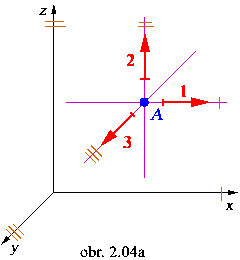
Hmotný bod v priestore má tri posuvné
(translačné) stupne voľnosti pohybu 1-2-3
(napr. v smere osi vzťažného súradnicového systému). Kedže hmotný bod nemá definovaný tvar
(je len abstrakciou malej časti telesa), rotačné stupne voľnosti sa mu neprisudzujú.
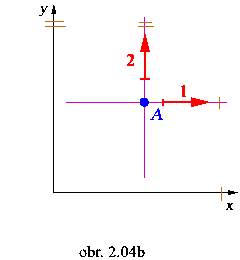
Hmotný bod v rovine má dva stupne voľnosti
1-2.
Priestor n = 3°
|
Rovina n = 2°
|
Teleso má v priestore tri posuvné a tri
rotačné stupne voľnosti. Má teda 6 stupňov voľnosti pohybu v priestore (n=6°).
Teleso má v rovine dva posuvné a jeden rotačný (okolo
osi z) stupeň voľnosti (n=3°). Pohyb telesa je viazaný na rovinu xy.
Ak na teleso pôsobí nerovnovážna silová sústava, teleso je v pohybe.
Aby sa nemohlo pohybovať, treba mu odobrať minimálne všetky stupne voľnosti pohybu
väzbami. Väzbové reakcie spolu s vonkajšími zaťažujúcimi silami budú tvoriť rovnovážnu
silovú sústavu a teleso bude v statickej rovnováhe. Väzbové reakcie vo väzbe pôsobia v
smere odobraného stupňa voľnosti pohybu a ich veľkosť a orientácia je závislá na
vonkajších silách. Pri ich výpočte ich spravidla vkladáme v kladnom zmysle - v zhode s orientáciou vzťažného
súradnicového systému, a označujeme ich: RA , RAx ,
MA , Ax , ...
Je definovaná vzťahom: i=n-r , kde n je počet stupňov
voľnosti pohybu telesa (v priestore n=6°; v rovine n=3°), r je počet stupňov voľnosti
odobratých väzbami.
Môžu nastať prípady uloženia:
a) i = 0 : |
teleso má väzbami odobrané všetky možné stupne voľnosti pohybu -
staticky určité uloženie |
b) i > 0 : |
teleso nemá odobrané všetky stupne voľnosti, to znamená, že má pohyblivé uloženie
- staticky podurčené. Toto uloženie je z hľadiska
statickej stability telesa neprípustné. |
c) i < 0 : |
teleso má odobratý väčší počet stupňov voľnosti pohybu ako ich v skutočnosti má
- statický neurčité (preurčené) uloženie. |
Ak je teleso uložené staticky určito, na výpočet väzbových reakcii
postačujú statické podmienky rovnováhy. Pri staticky neurčitom uložení je potrebné
statické podmienky rovnováhy doplniť o ďalšie rovnice, vyplývajúce z deformácie telesa.
a) Priestorové úlohy
a1) Väzba odoberajúca r=1° voľnosti, čiže
i=6°-1°=5° - teleso má ešte 5° stupňov voľnosti
pohybu. Teleso (guľa) - jeho pohyb je viazaný na rovinu xz v stykovom bode
A.
|
a2) Väzba odoberajúca r=2° voľnosti, čiže
i=6°-2°=4° - teleso má ešte 4° stupne voľnosti pohybu.
Teleso (valec) - jeho pohyb je viazaný na rovinu xz cez stykovú priamku. Väzba
odoberá posuv v smere osi y a rotáciu okolo osi
x.
|
a3) Väzba odoberajúca r=3° voľnosti, čiže
i=6°-3°=3° - teleso má ešte 3° stupne voľnosti pohybu.
Teleso(guľa) - jeho pohyb je viazaný na styk s priestorovou plochou. Väzba odoberá všetky
tri posuvné stupne voľnosti pohybu.
|
a4) Väzba odoberajúca r=4° voľnosti, čiže
i=6°-4°=2° - teleso má ešte 2° stupne voľnosti pohybu.
Väzba umožňuje telesu posuv v smere osi x a rotáciu okolo osi x.
|
a5) Väzba odoberajúca r=5° voľnosti, čiže
i=6°-5°=1° - teleso má jeden stupeň voľnosti pohybu -
posuv v smere osi x.
|
a6) Väzba odoberajúca r=6° voľnosti, čiže
i=6°-6°=0°
|
b) Roviné úlohy
VÄZBA |
ZNAČKA |
VÄZBOVÁ REAKCIA |
b1) posuvný kĺb:
i=3°-1°=2° Väzba odoberá posuv v smere osi y.
b2) pevný kĺb: i=3°-2°=1°
Väzba odoberá posuv v smere osi x a y.
b3) dokonalé votknutie:
i=3°-3°=0°
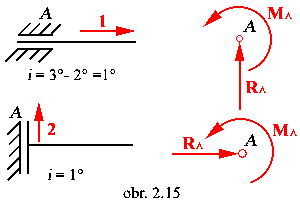
c) Špeciálne väzby
posuvné votknutie |
 |
väzba prútom (lanom)
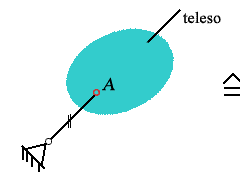
|
Odoberá jeden posuvný stupeň voľnosti v smere
osi prúta. (lana). Jeden prút odoberá 1 stupeň voľnosti
pohybu.
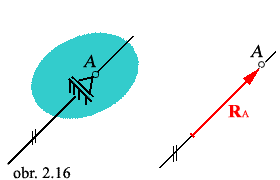
|
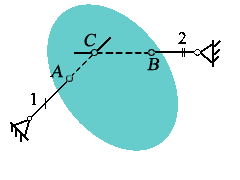
|
Dva prúty odoberajú dva stupne voľnosti.
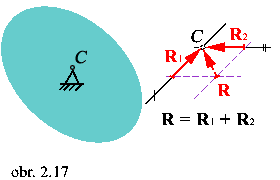
|
Poznámka: Každý pridaný prút odoberá ďalší stupeň voľnosti
pohybu, jeho os však nesmie prechádzať spoločným priesečníkom osi dvoch predchádzajúcich
prútov. Ako už bolo spomenuté, upevnenie lanom je väzba
jednosmerná.
Stupne voľnosti sa telesu odoberajú kombináciou základných typov väzieb.
Budeme predpokladať tzv. ideálne väzby, pri ktorých sa zanedbáva
trenie a ich čiastočná poddajnosť. Pri veľmi presných výpočtoch je nutné túto neideálnosť
väzieb zohľadniť, avšak pre väčšinu technických výpočtov je predpoklad ideálnej väzby
prípustný.
a) Staticky určité uloženie telesa v rovine: i = n - r = 0°
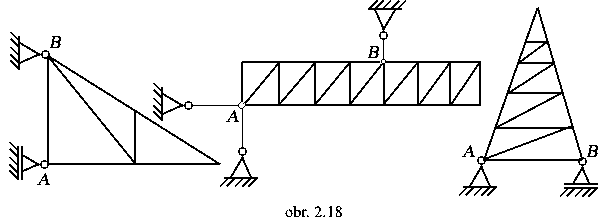
a1) prútové sústavy
|
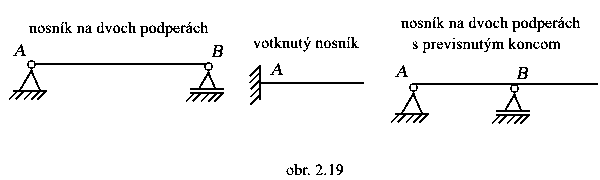
a2) nosníky
|
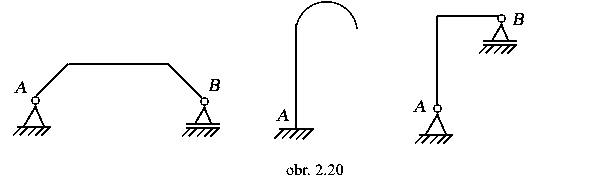
a3) lomené nosníky a zakrivené prúty
|
b) Staticky neurčité (preurčené) uloženie telesa v rovine: i = n - r < 0°
b1) prútové sústavy
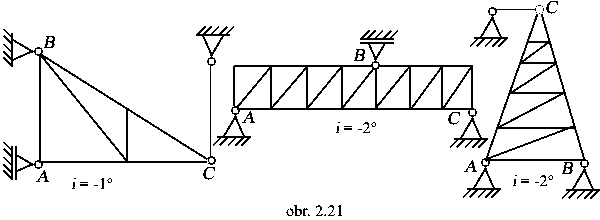 |
b2) nosníky
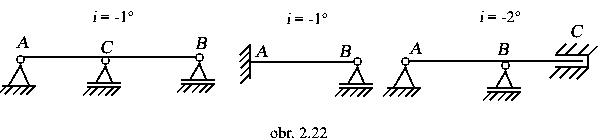 |
b3) lomené nosníky a zakrivené prúty
 |
Poznámky:
Staticky určité uloženie zabezpečuje stabilné (tuhým pohybom nepohyblivé)
upevnenie telesa. Pretože väzbové reakcie možno určiť zo statických podmienok
rovnováhy, riešenie staticky určitých úloh je jednoduché. Ako uvidíme neskôr, najväčšou
výhodou tohoto uloženia je, že teplotné namáhanie vyskytujúce sa v silnoprúdových a
energetických zariadeniach nespôsobuje vznik dodatočných vnútorných síl, ktoré môžu
spôsobiť mechanické poškodenie konštrukcie. Staticky určitá konštrukcia je však tuhostne
poddajnejšia (vykazuje väčšie mechanické deformácie).
Staticky neurčité (preurčené) uloženie spravidla vystužuje konštrukciu. Na statický
výpočet však nepostačujú len statické podmienky rovnováhy, ale podľa stupňa statickej
neurčitosti je ich nutné doplniť o tzv. deformačné podmienky.
Statický výpočet týchto konštrukcií analytickými metódami je preto obtiažnejší. Použitie
numerických metód (napr. metóda konečných prvkov - MKP) však tento problém odstraňuje.
Teplotné namáhanie (elektrické teplo, slnečné žiarenie, horúce pracovné médium) však
predstavuje aj z hľadiska pevnosti konštrukcie nezanedbateľný nepriaznivý faktor.
Dokonale tuhé teleso uložené staticky určito, resp. neurčito (preurčene)
sa pri zaťažení akýmikoľvek vonkajšími silami nepohybuje. Vonkajšie sily sú s väzbovými
reakciami v statickej rovnováhe. Existujú však výnimky z tohto pravidla. Táto výnimka je
spôsobená špecialnou vonkajšou silovou sústavou, resp. špeciálnou kombináciou vonkajších
väzieb.
a) Rovnováha staticky podurčene uloženého telesa
Teleso môže byť v statickej rovnováhe v prípade n < r »
i = n - r > 0° vtedy, keď výslednica vonkajších síl pôsobí tak, že môže nastať
statická rovnováha medzi ňou a výslednicou väzbových reakcií. Tento stav možno
dokumentovať nasledovnými príkladmi:
a1) prípad uloženia: n = 3° ; r =
1° ; i = 2°
Telesu zostali v rovine dva stupne voľnosti. Výslednica
vonkajších síl a väzbová reakcia ležia na spoločnej nositeľke, pričom platí: R = -
A
a2) prípad uloženia: n = 3° ; r =
2° ; i = 1°
Teleso má odobraté dva stupne voľnosti pohybu dvoma prútmi,
alebo dvoma bodovými stykmi, pričom nositeľky väzbových reakcií A a B sa
pretínajú v bode C. Ak výslednica vonkajších síl R prechádza tým istý bodom,
potom platí silová rovnica rovnováhy R + A + B + ... = 0 a teleso je v statickej
rovnováhe.
Sily A, B a R tvoria centrálnu rovinnú rovnovážnu silovú sústavu.
b) Statická nerovnováha staticky určito, resp. staticky neurčito (preurčene) uloženého
telesa.
V dôsledku nesprávnej kombinácie väzieb je uloženie telesa nestabilné
(teleso sa môže pohybovať). Zle zvolené väzby neplnia svoju funkciu - nazývajú sa
pasívne väzby.
b1) prípad uloženia n = 3° ; r =
3° ; i = 0°
Teleso je uložené staticky určito tak, že nositeľky väzbových
reakcii A, B a C sa pretínajú v bode C. Ak výslednica vonkajších
síl R ide mimo bod C, teleso sa môže okolo bodu D virtuálne pootočiť.
Pridaním ďalšej pasívnej väzby sa situácia nemení. Príkladom je uloženie
hriadeľa točivého stroja v ložisku. Pasívne väzby sú cez styčné plochy hriadeľa a
ložiska, vplyvom výslednej elektromagnetickej sily sa rotor v ložisku otáča. Špeciálne
prípady uloženia sa však využívajú pri konštrukcii mechanizmov vykonávajúcich predpísaný
pohyb (napr. pohony, roboty, mechatronické systémy, ...).
Poznámka:
Väzby treba voliť tak, aby
vznikla stabilná rovnováha, t.j. aby nenastal prípad špecialnej rovnováhy. V opačnom
prípade každá zmena vonkajších síl spôsobí tuhý pohyb konštrukcií, ktorý je pri
statických systémoch neprípustný.
Postup výpočtu väzbových reakcií staticky
určitých prípadov uloženia:
1) |
Odstránime všetky vonkajšie väzby a nahradíme ich väzbovými reakciami. Väzby
vkladáme do uvoľnených bodov v smere odobratého stupňa voľnosti, resp. v smere osi
zvoleného vzťažného súradnicového systému, a orientujeme ich kladne, t.j. kladné
väzbové sily sú orientované v zhode s orientáciou osi súradnicového systému a kladný
väzbový moment v zmysle pravidla pravej ruky. |
2) |
Pre uvoľnené teleso zostavíme statické podmienky rovnováhy (pre priestorovú úlohu
6 rovníc, pre rovinnú úlohu 3 rovnice), z ktorých vypočítame všetky väzbové reakcie.
Ak z rovníc rovnováhy dostaneme väzbovú reakciu s kladným znamienkom, potom v
skutočnosti pôsobí v tom zmysle (orientácia), ako sme ju do statického systému
vložili. Ak väzbovú reakciu dostaneme so záporným znamienkom, v skutočnosti pôsobí v
opačnom zmysle. |
Poznámka: - |
Skúšku správnosti výpočtu väzbových reakcií treba vykonať
pomocou ďalšej rovnice rovnováhy (napr. momentová podmienka rovnováhy k inému
ľubovolnému bodu telesa). |
- |
Pri rovinných úlohách sa doporučujú používať prednostne momentové
podmienky rovnováhy k bodu, kde pôsobia väzbové reakcie, a silové rovnice
rovnováhy treba použiť na skúšku správnosti výpočtu. |
Príklad č. 2.1: |
Treba určiť väzbové reakcie v upevnení ramena stožiara vn uloženého a
zaťaženého silou F podľa obrázka. |
Upevnené teleso ramena
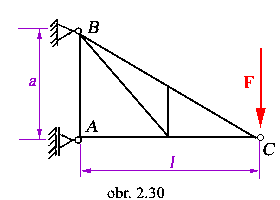 |
Uvoľnené teleso ramena s vloženými väzbovými reakciami v kladnom
zmysle
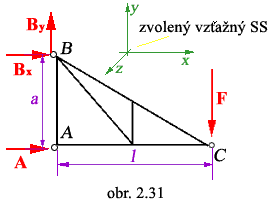 |
Statické podmienky rovnováhy (rovinná úloha)
Pre tri neznáme reakcie treba napísať tri rovnice rovnováhy.
Momentová rovnica rovnováhy k bodu A (momenty všetkých síl točia okolo osi z, kolmej
na rovinu papiera):
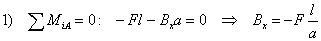
Momentová rovnica rovnováhy k bodu B:
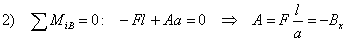
Silová rovnica rovnováhy v smere osi y:
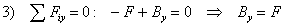
Skúška správnosti: |
 |
Väzbové reakcie sú vypočítané správne. Reakcia Bx má v
skutočnosti opačnú orientáciu, ako sme predpokladali.
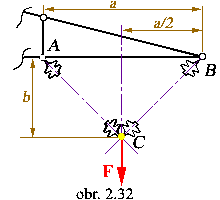
Priklad č. 2.2:
Treba určiť väzbové reakcie v uchyteniach izolátorov na rameno stožiara.
Skutočný systém
 |
Statický systém
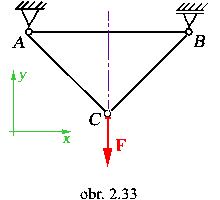 |
Uvoľnený statický systém
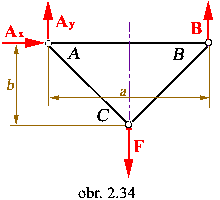 |
Na výpočet väzbových reakcii možno použiť tieto tri rovnice rovnováhy:
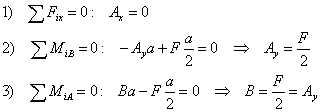 |
Skúška správnosti:
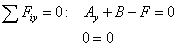 |
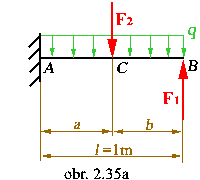
Príklad č.2.3: Treba určiť väzbové reakcie v
uložení votknutého nosníka.
 |
Uvoľnený sytém
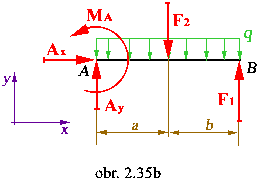 |
| Rovnice rovnováhy: |
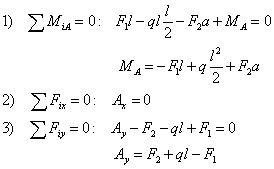 |
| Skúška správnosti: |
 |
| Poznámka: |
Ak na teleso pôsobí väčší počet rôznych vonkajších zaťažení, skutočnú orientáciu
väzbových reakcií možno určiť až po dosadení konkrétnych hodnôt vonkajších síl. Ak
napr. F1 = F2 = F = 1000 N a
q = F/l potom: |
|
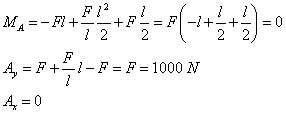 |
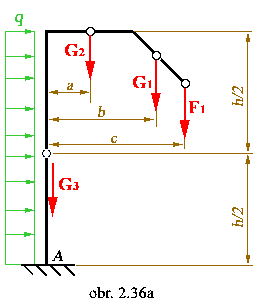
| Príklad č.2.4: |
Treba určiť väzbové reakcie v upevnení stĺpa pouličného osvetlenia zaťaženého podľa
obrázku (F1 - tiaž svietidla, G1, G2,
G3 - vlastná tiaž časti stĺpa, q - sila vetra). |
 |
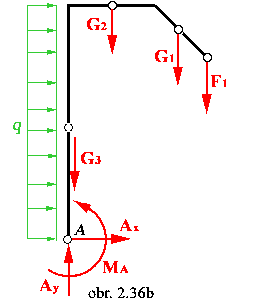
Uvolnený systém
 |
| Podmienky rovnováhy: |
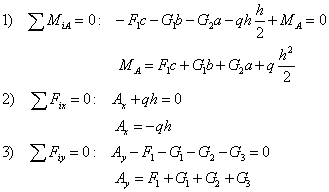 |
| Príklad č.2.5: |
Treba určiť väzbové reakcie v uchyteniach vodiča vn, zaťaženého vlastnou tiažou
sústredenej do ťažiska vodiča. |
| Statická určitosť: |
i = n - r = 3 - 4 = 1° »
úloha je 1-krát staticky neurčitá. |
| Podmienky rovnováhy: |
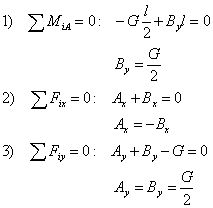 |
Veľkosť reakcii Ax a Bx je
závislá na tzv. vnútorných silách, ktorých výpočtom sa
budeme zaoberať nekôr v rámci pružnosti a pevnosti materiálu. Statické podmienky
nepostačujú na výpočet väzbových reakcii pri staticky neurčitom uložení telesa.
|

 Výučba
Mechaniky
Výučba
Mechaniky