Učebný cieľ kapitoly

Po preštudovaní tejto kapitoly by ste mali ovládať:

• Rovnováhu sústavy hmotných bodov
• Riešiť prútovku ako sústavu hmotných bodov
• Rozdelenie prútových sústav
• Statickú určitosť prútoviek
• Metódy statickej analýzy prútoviek

3.1 ROVNOVÁHA SÚSTAVY HMOTNÝCH BODOV

Hmotný bod
je v statickej rovnováhe, keď výslednica síl pôsobiacich na hmotný bod je rovná nule.

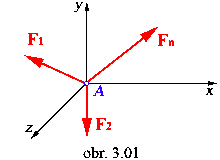Rovnováhu hmotného bodu možno vyjadriť statickými podmienkami rovnováhy:

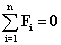
Skalárny tvar (zložkový) rovníc rovnováhy je:

a) v priestore

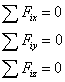
b) v rovine

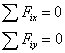
Sústava hmotných bodov
(tvorená dvoma a viacerými hmotnými bodmi) je v statickej rovnováhe, keď je v statickej rovnováhe každý bod sústavy. Napr.: pre sústavu troch hmotných bodov platí:

3.2 PRÚTOVKA AKO SÚSTAVA HMOTNÝCH BODOV

Prútová sústava vznikne spojením viacerých prútov (tyčí) v spoločných bodoch - styčníkoch. Prierezová plocha prútov môže byť rôzna a po dĺžke prúta je spravidla konštantná. Za predpokladu, že styčníky predstavujú rotačné kĺby bez trenia, prúty prenášajú len osovú vnútornú silu. Tento predpoklad je vyhovujúci, ak dĺžka prúta v porovnaní s jeho prierezovou plochou je výrazne prevažujúcim rozmerom prúta. Potom je možné skutočné spojenie prútov (skrutkový spoj, zvarovaný spoj, nitovaný spoj, a iné) považovať za tzv. ideálne kĺby.
Príklady prútoviek: stožiare vn, osvetľovacie veže a rampy, nosníky a stĺpy v rozvodniach a transformačných staniciach, anténne systémy, a pod.

a) spojenie troch prútov

b) spojenie štyroch prútov

Mechanický model rovinnej prútovej sústavy
Rovinná prútová sústava: všetky prúty i vonkajšie sily ležia v jednej rovine. Prúty predstavujú vnútorné väzby medzi styčníkmi (hmotnými bodmi).

Predpoklad pre zaťaženie
Prútovka je zaťažená len sústredenými silami s pôsobiskom v styčníkoch. Spojité zaťaženia, ako je vlastná tiaž, sila vetra, tiaž námrazy atď., je preto potrebné ekvivalentne pretransformovať do sústredených síl pôsobiacich v styčníkoch.

Predpoklad pre prúty
Prúty predstavujú vnútornú väzbu medzi dvoma hmotnými bodmi - styčníkmi. Tieto väzby odoberajú hmotnému bodu jeden stupeň voľnosti pohybu v smere osi prúta. Ak odstránime vnútorné väzby medzi hmotnými bodmi, musíme ich nahradiť vnútornými väzbovými reakciami, ktoré sa nazývajú osové sily v prútoch a označujú sa písmenom P_i , kde i je číslo prúta.

Predpoklad pre osové sily v prútoch
Prúty sústavy sú namáhané osovými silami na ťah, alebo tlak. Ich veľkosť a orientácia je závislá na geometrii prútovej sústavy, zaťažujúcich vonkajších silách a uložení prútovky prostredníctvom vonkajších väzieb.
Kladná osová sila (ťah) je orientovaná von z mysleného rezu prúta, resp. von zo styčníka. Záporná osová sila (tlak) je orientovaná v zmysle do mysleného rezu, resp. do styčníka.

Odstránením prútov a ich náhradou osovými silami (pri výpočtoch budeme vždy predpokladať kladnú osovú silu v prúte), ako aj odstránením vonkajších väzieb a ich náhradou vonkajšími väzbovými reakciami, dostaneme sústavu hmotných bodov v rovine:

Sústava hmotných bodov

Táto sústava je v statickej rovnováhe, ak je v rovnováhe každý hmotný bod, t.j. keď sú splnené statické podmienky rovnováhy (vektorové rovnice):

Ak tieto vektorové rovnice rovnováhy rozpíšeme do zložkového tvaru, dostaneme desať skalárnych rovníc pre výpočet desiatich neznámych síl (7 osových síl P₁ až P₇ a troch väzbových reakcii
E_x , E_y a A).

3.3 ROZDELENIE PRÚTOVÝCH SÚSTAV

Podľa geometrie prútovky a jej zaťaženia rozoznávame:

1. jednoosové (jednorozmerné) prútovky
2. rovinné prútovky
3. priestorové prútovky

Jednorozmerná prútovka
obsahuje prúty s paralelnými osami, pričom zaťažujúce sily pôsobia v smere osi prútov.

Ak dĺžka jednotlivých častí tiahla na obr.3.11 je dominantným rozmerom oproti ich prierezovej ploche, potom ju možno nahradiť mechanickým modelom jednoosovej prútovky (obr.3.12).

Prúty, styčníky i vonkajšie sily rovinnej prútovky ležia v jednej rovine.

Prúty, styčníky i vonkajšie sily priestorovej prútovky sú všeobecne rozptýlené v priestore.

Špeciálne priestorové prútovky, ktorých prúty ležia vo vzájomne na seba kolmých rovinách možno rozložiť na rovinné prútové sústavy. Prúty v každej z rovín sústavy prenášajú silové účinky síl ležiacich v tej istej rovine. Tým možno riešenie špeciálnej priestorovej prútovky rozložiť na riešenie viacerých rovinných úloh. V ďalšej časti učebnice sa budeme zaoberať výlučne rovinnými prútovými sústavami.

3.4 STATICKÁ URČITOSŤ PRÚTOVIEK

Statická analýza rovinných prútoviek závisí aj od statickej určitosti úlohy. Pri prútovkách rozlišujeme medzi vonkajšou a vnútornou statickou určitosťou. Prútová sústava je staticky určitá, ak je staticky určitou sústavou tak po vnútornej ako aj po vonkajšej stránke. V opačnom prípade pôjde o staticky neurčitú (preurčenú, resp. podurčenú) prútovku.

Vonkajšia statická určitosť i_vo je závislá od počtu odobraných stupňov voľnosti celej prútovky (ako jednému telesu) vonkajšími väzbami, a vypočítame ju podľa vzťahu i_vo = 3 - n , kde n je počet stupňov voľnosti pohybu odobratých vonkajšími väzbami. Prútovka je uložená po vonkajšej stránke staticky určito, ak i_vo = 0. V opačnom prípade ide o staticky neurčité uloženie. Z hľadiska statiky prútovky je nutné odobrať minimálne tri stupne voľnosti aktívnymi väzbami.

Vnútornú statickú určitosť možno stanoviť zo vzťahu: i_vn=3p - 2(nk_n + ... + 4k₄ + 3k₃ + 2k₂ + k₁ ), kde p je počet prútov sústavy, k_n je počet styčníkov určitého typu:

k₁ - jednoduchý styčník - v styčníku sa spájajú dva prúty
k₂ - dvojnásobný styčník - v styčníku sa spájajú tri prúty
k_n - n-násobný styčník - styčníku sa spája (n+1) prútov

Rovinná prútová sústava je staticky určitá, keď i_vo=0 a i_vn=3.

Ak je prútová sústava staticky určitá, na výpočet osových síl a vonkajších väzbových reakcii postačujú statické podmienky rovnováhy. Teplotné namáhanie, poddajnosť vonkajších väzieb ako aj výrobná nepresnosť nespôsobujú na rozdiel od staticky neurčitých úloh vznik vnútorných síl a väzbových reakcií. Pri staticky neurčitých prútovkách musíme statické podmienky rovnováhy doplniť deformačnými podmienkami. Veľkosť osových síl v staticky neurčitej prútovke je teda závislá aj na veľkosti prierezov jednotlivých prútov.

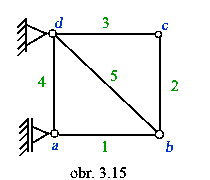
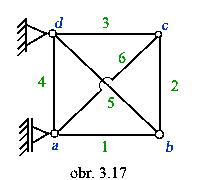
Príklad:
Vypočítajte statickú určitosť prútoviek podľa obrázku.

ivo=3-2-1=0 ivn=3.5-2(2.2+2)=15-12=3 - staticky určitá úloha	ivo=3-3=0 ivn=3.4-2(4)=12-8=4 ivn>3 - prútovka je pohyblivá (mechanizmus s jedným stupňom voľnosti pohybu)	ivo=0 ivn=3.6-2(2.4)=18-16=2 ivn<3 - staticky neurčitá úloha (jeden krát)

Pravidlo:
Rovinná prútovka je po vnútornej stránke staticky určitá, ak jej tvar je tvorený spojením prútov do trojuholníka.

3.5 METÓDY STATICKEJ ANALÝZY PRÚTOVIEK

Metódami statiky možno riešiť len staticky určité prútové sústavy. Týmito metódami možno určiť vonkajšie väzbové reakcie a vnútorné sily v prútoch. Na výpočet deformácie prútoviek, a tým aj na analýzu staticky neurčitých úloh je potrebné použiť vzťahy z oblasti pružnosti a pevnosti materiálu. V ďalšom sa preto v rámci statiky budeme zaoberať riešením len staticky určitých prútoviek. Cieľom riešenia bude výpočet statickej určitosti, vonkajších väzbových reakcií a osových síl v prúte. V ďalších kapitolách sa budeme zaoberať výpočtom deformácie prútoviek ako aj riešením staticky neurčitých úloh.

Metódy riešenia prútoviek sa všeobecne delia na:

1. analytické
2. vektorové (grafické)
3. numerické (počítačovo orientované)

Každá skupina týchto metód obsahuje viacero konkrétnych postupov riešenia. Nástup počítačov urýchlil prudký rozvoj numerických metód mechaniky. Prednosti numerických metód, napr. metóda konečných prvkov (MKP), posunuli do úzadia v minulosti veľmi často používané grafické metódy (napr.Cremonov plán, Wiliottov plán, atď.), ktoré sa v súčasnosti takmer prakticky nepoužívajú. Kvôli fyzikálnej podstate problému uvedieme v ďalšom dve najpoužívanejšie analytické metódy riešenia statiky prútových sústav, a síce styčníkovú a priesečnu metódu. Tieto metódy možno výhodne použiť na kontrolu výsledkov získaných počítačovo orientovanými metódami.

3.5.1 Styčníková metóda

Princíp metódy
vychádza z podmienok rovnováhy sústavy hmotných bodov. Hmotný bod = uvoľnený styčník, v ktorom pôsobia známe vonkajšie sily a vonkajšie väzbové reakcie, ako aj neznáme osové sily styčníkom spojených prútov.

1. Odstránime vonkajšie väzby a z podmienok rovnováhy celej prútovky vypočítame vonkajšie väzbové reakcie
2. Z podmienok rovnováhy síl uvoľneného styčníka vypočítame neznáme osové sily.

Poznámka:
Pri riešení rovnováhy vychádzame zo styčníka, v ktorom pôsobia vonkajšie sily (alebo známe vonkajšie reakcie), a maximálne dve neznáme osové sily.

Príklad:
Vypočítajte statickú určitosť, väzbové reakcie ako aj osové sily v prútoch.

a) statická určitosť ivo=3-3=0 ivn=3.3-2(3)=3 - prútovka je staticky určitá
b) vonkajšie väzbové reakcie
c) osové sily rovnováha styčníka c:
rovnováha styčníka a:

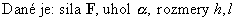
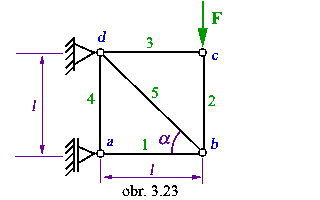
Príklad:
Vypočítajte osové sily v prútoch. Dané je: F, l.

a) statická určitosť: ivo=0 , ivn=3.5-2(2.2+2)=3 - prútovka je staticky určitá
b) vonkajšie väzbové reakcie:
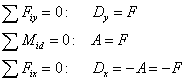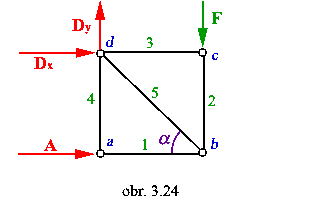c) osové sily: rovnováha styčníka c
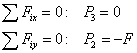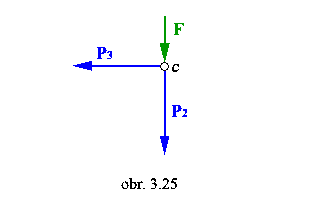rovnováha styčníka a
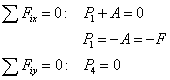rovnováha styčníka b
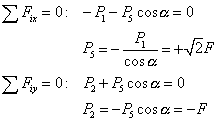d) zhrnutie výsledkov Prút číslo 1 2 3 4 5 Pi -F -F 0 0 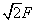Najviac namáhaný (na ťah) je prút č.5

Poznámka:
Prútom, v ktorých je nulová sila sa hovorí nulové prúty. Aj keď tieto prúty nie sú namáhané pre daný zaťažovací stav, musia byť v prútovke prítomné, pretože držia tvar prútovej sústavy.

Prípady nulových prútov (nulové prúty sú označené šikmou čiarou):
- dva prúty spojené v nezaťaženom styčníku
- dva prúty zaťažené silou ležiacej na osi niektorého prúta
- tri prúty spojené v nezaťaženom styčníku, pričom osi dvoch prútov sú totožné

3.5.2 Priesečná metóda (Ritterov rez)

Princíp metódy
vychádza z momentových podmienok statickej rovnováhy telesa, resp. jeho jednej odrezanej časti mysleným rezom cez maximálne tri prúty nepretínajúce sa v jednom bode. Vložené osové sily musia byť v rovnováhe s vonkajšími silami pôsobiacimi na odrezanú časť prútovky. Momentové podmienky rovnováhy odrezanej časti prútovky treba písať k bodom, ktoré sú priesečníkom osi dvoch prerezaných prútov. V niektorých úlohách takáto možnosť neexistuje, v takom prípade treba použiť silové podmienky rovnováhy.

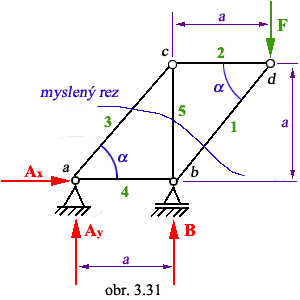
Priklad: Vypočítajte sily P₁, P₃ a P₅, keď je dané: F = 5 kN, a = 3 m

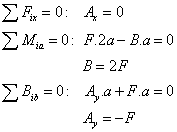
a) statická určitosť: ivo = 0 ; ivn = 3 - prútovka je staticky určitá b) väzbové reakcie: c) Skúška správnosti:

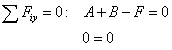
d) osové sily:
Prútovku rozrežeme mysleným rezom na dve časti. Osové sily P₁, P₃, P₅ možno vypočítať zo statických podmienok rovnováhy jednej z odrezanej časti (treba si zvoliť jednoduchšiu časť prútovky). Tu je výhodnejšia pravá časť prútovky, do rezov vložíme kladné osové sily.

Z momentovej podmienky k bodu C, v ktorom sa pretínajú nositeľky síl P3 a P5 možno určiť silu P1: Z momentovej podmienky rovnováhy k bodu b možno určiť silu P3: Keďže sily P3 a P1 sa pretínajú v nekonečne, na výpočet sily P5 musíme použiť rovnicu rovnováhy síl:

Záver:
Prúty č.1 a 5 sú tlačené, prút č.3 je namáhaný na ťah silami:

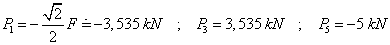
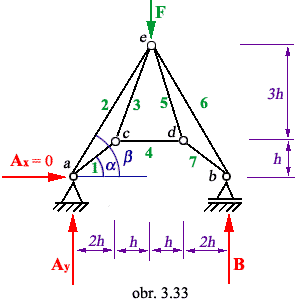
Príklad: Vypočítajte silu P₄. Dané je: F, h

a) statická určitosť: iv0 = 3-2-1 = 0 ivn = 3.7-2(1.3+2.2+2.1) = 3 - prútovka je staticky určitá b) väzbové reakcie:

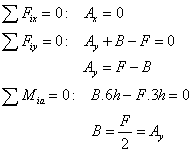
c) osová sila P₄:
Mysleným rezom cez prúty 2, 3 a 4 rozdelíme teleso na dve časti. Hľadané osové sily určíme napr. z podmienok ľavej odrezanej časti telesa.

Momentová rovnica rovnováhy k priesečníkom osových síl P₂ a P₃:

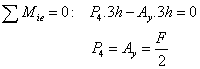
Podobným spôsobom možno určiť ďalšie požadované osové sily.

Príklad:
Vypočítajte osové sily P₃, P₄ a P₅ v prútoch ramena stožiara vysokého napätia. Dané je: F, a, b, .

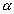Osové sily vypočítame z podmienok statickej rovnováhy pravej časti prútovky.

Z geometrie a zaťaženia prútovky je zrejmé, že aj prút č.6 je nulovým prútom. Z rovnováhy styčníka C potom vyplýva, že P₂ = P₅, a z rovnováhy styčníka B vyplýva, že P₁ = P₃. Keďže P₄ = 0, potom z rovnováhy styčníka D vyplýva, že aj prút č.7 je nulovým prútom, teda P₇ = 0.