|
Učebný cieľ kapitoly
Po preštudovaní tejto kapitoly by ste mali ovládať:
- Čo je obsahom predmetu "Pružnosť a pevnosť", aké je jeho postavenie v odbore
ESI.
- Čo je to poddajné kontinuum.
- Čím sú charakterizované vnútorné sily a mechanické napätia.
- Princíp metódy mysleného rezu.
- Ako je definovaný vektor mechanického napätia, normálové a šmykové napätie.
- Čo sú to základné prípady namáhania, a ako ich delíme.
- Aké sú základné zložky deformácie a ich matematické a fyzikálne vyjadrenie.
- Pracovný diagram trhacej skúšky, Hookov zákon a modul pružnosti.
- Ako je definované priečne zúženie.
- Odvodenie vzťahov pre energiu napätosti normálových a šmykových napätí.
- Odvodenie 1. Castiglianovej vety a jej fyzikálny význam.
- Na čo slúži pevnostná podmienka, čo je to dovolené namáhanie a miera bezpečnosti.
Predmet "Pružnosť a pevnosť" sa zaoberá rovnováhou
deformovateľného (poddajného) telesa a skúma účinky pôsobenia zaťažujúcich síl na
poddajné teleso.
Mechanické súčiastky strojov a zariadení, prenášajúce účinky zaťažujúcich
síl, sú zhotovené z konštrukčných materiálov vyznačujúcich sa základnými mechanickými
vlastnosťami:
- Pružnosť materiálu je schopnosť materiálu nadobúdať, po
prerušení pôsobenia zaťažujúcich síl, svoj pôvodný tvar.
- Pevnosť materiálu je schopnosť materiálu odolávať
pôsobeniu zaťažujúcich síl bez prerušenia.
Na rozdiel od statiky sa pružnosť a pevnosť zaoberá prvkami konštrukcie,
ktoré pri vzájomnom pôsobení na seba menia svoje rozmery a tvar. Táto zmena sa nazýva
deformácia. Hmotnému telesu schopnému sa deformovať hovoríme
poddajné teleso. Mechanické vlastnosti pružnosť a pevnosť
úzko súvisia s účinkami zaťažujúcich síl na poddajné teleso. Predmet Pružnosť a pevnosť
skúma odozvu deformovateľného telesa na pôsobenie zaťažujúcich síl. Po zostavení
matematického modelu daného konštrukčného prvku je jej cieľom navrhnúť jeho optimálne
rozmery tak, aby nenastala porucha materiálu prekročením jeho pevnosti alebo neprimeranou
deformáciou.
Obsah tejto časti predmetu "Mechanika a Termomechanika" je
zameraný na poznatky o silovom pôsobení a jeho účinkoch na poddajné hmotné body a telesá
pevnej fázy. Obsahuje aplikačné výpočtové metódy na bezpečný návrh niektorých konštrukčných
prvkov a systémov silnoprúdovej elektrotechniky a elektroenergetiky, s poukázaním na možné
príčiny mechanických porúch a ich dôsledkov na bezpečnú a spoľahlivú prevádzku.
Materiál konštrukčných prvkov možno rozdeliť do dvoch skupín.
- kryštalické
- amorfné
Kryštalické materiály pozostávajú z veľkého počtu malých zŕn. Každé zrno
tvorí sústava atómov pravidelne v radoch rozložených, ktoré tvoria kryštalickú mriežku.
Naproti tomu amorfné materiály nemajú pravidelne usporiadané atómy. Ak by sme pristupovali ku
skúmaniu účinku zaťažujúcich síl na poddajné teleso mikroskopickým
spôsobom, narazili by sme na problémy spojené najmä so zložitosťou
matematického modelu a s odlišnosťami od ideálneho kryštalického zloženia konštrukčných
materiálov (dané nerovnomernosťou kryštalizácie, nečistotami a vmestkami v kryštalickej
mriežke). Preto v pružnosti a pevnosti abstrahujeme od skutočného zloženia hmotného
telesa - aplikujeme makroskopický prístup. Hmotné poddajné
teleso budeme považovať za kontinuum.
Koncept kontinua je odvodený z matematiky.
Povieme, že systém reálnych čísiel je kontinuum. Medzi každými dvoma určitými číslami sú
iné čísla, vlastne medzi uvažovanými dvoma číslami existuje nekonečne veľa reálnych
čísiel. Intuitívne, čas môže byť reprezentovaný tromi systémami reálnych čísiel x, y, z.
Čas a priestor identifikujeme ako štvorrozmerné kontinuum. Rozšírením pojmu kontinua na
hmotu budeme hovoriť o spojitom rozdelení hmoty v priestore. Hmotné teleso bude takto
pozostávať z hmotných bodov, z ktorých každý obsahuje veľké množstvo elementárnych častíc
(atómov, elektrónov). Koncept materiálneho kontinua je matematickou abstrakciou
(idealizáciou) reálneho sveta a je aplikovateľný na problémy, v ktorých jasnosť štruktúry
sa môže zanedbať.
Jednotlivé časti konštrukcií v spojení s inými tvoria konštrukčný celok,
ktorý je buď v pokoji (napr. stožiar VN, zapuzdrený vodič, izolátor, osvetľovací systém,
nádoba reaktora, atď.), alebo v pohybe (časti točivých elektrických strojov a pohonov,
mechatronické systémy, atď.). Pritom prostredníctvom vzájomných dotykových plôch
prenášajú sily na seba. Sily ktorými pôsobia ostatné časti konštrukcie na uvažovanú
súčiastku, nazývame vonkajšímy silami, ktorými sme sa už
zaoberali v statike.
Vonkajšie zaťaženie možno ďalej deliť na
trvalé a dočasné. Trvalé
zaťaženie pôsobí po celý čas prevádzky konštrukcie, napr. jej vlastná tiaž a pod.
Dočasné zaťaženie len nejaký časový úsek, napr. tiaž montéra na stožiari VN a pod.
Podľa charakteru pôsobenia možno zaťaženie ešte rozdeliť na
statické a dynamické. Statické
zaťaženie vzrastá postupne od nuly až na vlastnú, menovitú hodnotu (napr. krútiaci moment
elektromotora na hriadeľ). Pôsobenie dynamických síl vzniká spravidla v krátkej časovej
perióde a pritom aj súčiastky, na ktoré dynamické sily pôsobia, sú obyčajne v
pohybe.
obr.4.1 Poddajné teleso
 |
Na obr. 4.1 vidíme poddajné kontinuum zaťažené silovou sústavou
F1, F2, ..., Fn. Teleso, ktoré malo
pred zaťažením tvar vyznačený plnou čiarou, sa po zaťažení zdeformuje do tvaru
vyznačeného čiarkovanou čiarou. (Deformácia telesa je pre názornosť nakreslená prehnane
veľká. Vo všetkých kapitolách tejto učebnice bude prijatý
predpoklad nekonečne malých deformácií.) Odozvou telesa na zaťažujúce sily je jeho
deformácia. Ak zaťažujúce sily (akcie aj reakcie) prestanú pôsobiť, pružnosť materiálu
spôsobí jeho návrat do pôvodného stavu. To znamená, že v prvkoch konštrukcie
vznikajú pôsobením vonkajších síl doplnkové vnútorné sily,
ktoré pôsobia proti úsiliu vonkajších síl porušiť konštrukčný prvok, alebo meniť jeho
tvar. V ďalšom budeme tieto sily nazývať vnútornými silami.
Keby sme teleso chápali mikroskopicky, atómy sa v mriežke udržiavajú vzájomne pôsobiacimi
medziatómovými silami. Vplyvom vonkajších síl sa vzdialenosti medzi atómami menia (teleso
sa deformuje), čo je spôsobené zmenou vzájomne pôsobiacích síl medzi atómami.
Analogicky pri makroskopickom prístupe nachádzajú sa hmotné body v telese v rovnováhe. Ak
začneme pôsobiť vonkajšími silami, hmotné body sa bránia vysunutiu zo svojej
rovnovážnej polohy - vznikajú už spomenuté vnútorné sily.
Tieto vnútorné sily sú, podobne ako pojem kontinua, matematickou abstrakciou, ktorú
zaviedli Cauchy a Euler.
Aby sa dal číselne charakterizovať stupeň účinku vonkajších síl na
deformovaný prvok, treba vedieť vypočítať veľkosť vnútorných síl. Na to sa v pružnosti a
pevnosti používa metóda jedného alebo viacerých myslených
rezov. Voľba ich počtu závisí od zložitosti riešenej úlohy.
Metóda mysleného rezu tkvie v
nasledujúcich úvahách:
Teleso na obr. 4.2 rozrežeme mysleným rovinným rezom 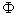 na dve konečné časti
A a B. na dve konečné časti
A a B.
obr.4.2 Metóda mysleného rezu
 |
Pôsobením vonkajších síl sa obe časti telesa usilujú oddeliť a
udržiavajú sa pohromade vzájomnými vnútornými silami pôsobiacimi medzi hmotnými
bodmi, ktoré sú na oboch stranách mysleného rezu. Na obr. 4.2 sú nakreslené
výslednice týchto síl. Vnútorné sily pôsobiace na časť A od časti B a vnútorné sily
pôsobiace na časť B od časti A sa podľa zákona akcie a reakcie sebe rovnajú
(Cauchyho-Eulerov princíp). Ak má nastať rovnováha každej z odrezaných častí, musia byť
vnútorné sily pôsobiace na časť A v rovnováhe s vonkajšími silami pôsobiacimi
na túto časť a rovnako i na časti B. Výslednicu vnútorných síl P nazývame
vektorom napätia a určíme ho zo statických podmienok
rovnováhy vonkajších a vnútorných síl a momentov síl.
Vnútorné sily sú vo všeobecnosti nepravidelne rozložené po priereze,
takže statické podmienky rovnováhy nestačia na určenie rozloženia vnútorných síl v
jednotlivých hmotných bodoch ležiacich v rovine mysleného rezu. Zo statických podmienok
rovnováhy možno určiť len výslednicu vnútorných síl.
Aby sme mohli lepšie porovnávať účinok vnútorných síl v rôznych
rezových plochách, zavádzame pomer vnútorných síl na jednotku prierezovej plochy, ktorý
nazývame mechanickým napätím.
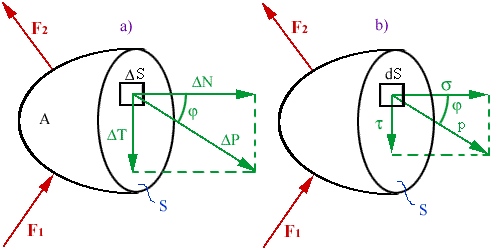
Vybratý hmotný bod si nahradíme pravouhlým elementárnym hranolčekom,
ktorého jedna plocha sa nachádza v rovine rezu a jej veľkosť je
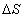 ,
obr.4.3. Na tejto plôške pôsobí elementárna vnútorná sila ,
obr.4.3. Na tejto plôške pôsobí elementárna vnútorná sila
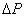 a s
normálou k rezovej rovine zviera uhol a s
normálou k rezovej rovine zviera uhol
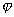 . Túto silu
rozložíme do normály a tangenty k rezovej rovine. Potom podľa obr.4.3 platí: . Túto silu
rozložíme do normály a tangenty k rezovej rovine. Potom podľa obr.4.3 platí:
obr.4.3 Pojem napätia
 |
Limita pomeru vnútorných síl
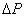 , ,
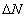 , ,
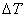 k
ploche k
ploche
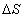 sa
nazýva napätie, jeho smer a zmysel sa zhoduje so smerom a zmyslom vnútornej sily a
ktorého rozmer je N.mm-2 (MPa), prípadne iné odvodené jednotky.
Napätie budeme v ďalšom texte označovať písmenami našej, resp. gréckej abecedy.
Označenie p budeme používať pre napätie ľubovolne
sklonené k vyšetrovanej plôške, písmenom sa
nazýva napätie, jeho smer a zmysel sa zhoduje so smerom a zmyslom vnútornej sily a
ktorého rozmer je N.mm-2 (MPa), prípadne iné odvodené jednotky.
Napätie budeme v ďalšom texte označovať písmenami našej, resp. gréckej abecedy.
Označenie p budeme používať pre napätie ľubovolne
sklonené k vyšetrovanej plôške, písmenom
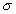 budeme označovať normálové napätie, ktoré je kolmé na
rovinu rezu a písmenom
budeme označovať normálové napätie, ktoré je kolmé na
rovinu rezu a písmenom
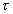 šmykové napätie, ktoré leží v rovine rezu obr.4.3
šmykové napätie, ktoré leží v rovine rezu obr.4.3
Jednotlivé napätia sú definované vzťahmi:
Normálovému napätiu priraďujeme tiež znamienko, a to:
kladné, keď zmysel sily
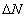 smeruje von z plochy rezu, a nazývame ho napätím ťahovým. Ak je zmysel sily
smeruje von z plochy rezu, a nazývame ho napätím ťahovým. Ak je zmysel sily
 opačný, priraďujeme mu znamienko záporné, a takéto
napätie nazývame tlakovým. Na orientácii šmykového napätia obvykle nezáleží,
ale len na jeho veľkosti.
opačný, priraďujeme mu znamienko záporné, a takéto
napätie nazývame tlakovým. Na orientácii šmykového napätia obvykle nezáleží,
ale len na jeho veľkosti.
Iné napätie ako ťahové, tlakové alebo šmykové na plôške
 nie je mysliteľné. Ich smer a veľkosť závisí od vonkajšieho zaťaženia a od veľkosti a
polohy plôšky
nie je mysliteľné. Ich smer a veľkosť závisí od vonkajšieho zaťaženia a od veľkosti a
polohy plôšky
 .
Pri každom druhu namáhania sa môžu vyskytovať iba tieto napätia, a to alebo
každé samostatne, alebo v kombinácii. .
Pri každom druhu namáhania sa môžu vyskytovať iba tieto napätia, a to alebo
každé samostatne, alebo v kombinácii.
Z rovníc napätia je zrejmé, že:
V bode C sme určili výslednicu vnútorných síl pre rezovu plochu S. Táto
výslednica P je v statickej rovnováhe s vonkajšími silami, pôsobiacimi na časť telesa
A obr.4.4.
obr.4.4 Zložky výslednice vnútorných síl
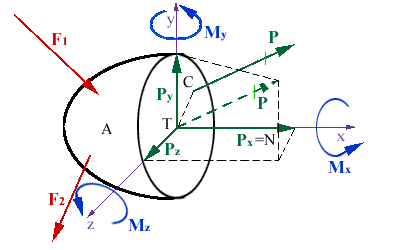 |
Preložme vnútornú silu P do ťažiska T plochy prierezu S a rozložme
ju do súradnicových osí x, y, z, z ktorých os x je kolmá na
rezovu rovinu. Tieto zložky výslednej vnútornej sily sú na obrázku vyznačené
Px, Py a Pz. Aby táto
transformácia sily bola ekvivalentná, treba k preloženej sile P pripojiť dvojicu
síl, ktorej zložky otáčavého účinku do súradných osí sú
Mx, My, Mz. Tak sme dostali v
ťažisku plochy prierezu šesť zložiek výslednice vnútorných síl (tri sily a tri momenty
síl). Ak pôsobí v ťažisku plochy S viac zložiek výslednice vnútorných síl ako
jedna, hovoríme o kombinovanom (zloženom) namáhaní. Ak
pôsobí v uvažovanom reze len jedna z uvažovaných zložiek, hovoríme o
jednoduchom (prostom) namáhaní. Podľa toho rozoznávame
päť základných (jednoduché, prosté, čisté) prípadov namáhaní: prostý ťah (tlak),
prostý šmyk, prosté krútenie, prostý ohyb, a vzper.
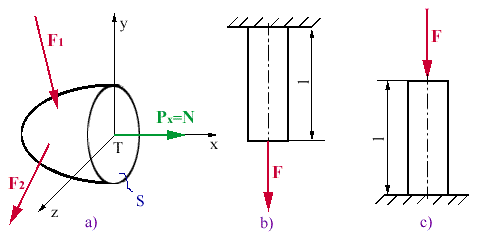
O prostom ťahu alebo tlaku hovoríme vtedy, ak v myslenom reze
pôsobí len zložka výslednice vnútorných síl Px = N
obr.4.5c. Najjednoduchším prípadom ťahového namáhania je tenká priama tyč,
konštantného prierezu namáhaná osovou silou F obr.4.5b. Najjednoduchším
prípadom tlakového namáhania je prípad podľa obr.4.5c. Pretože v myslenom reze
pôsobí výslednica vnútorných síl na normále k prierezu, pri ťahu, resp. tlaku
vzniká normálové napätie
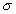 (+
(+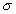 pre
ťah a - pre
ťah a -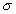 pre tlak). Takto sú namáhané napr. tyče (prúty) stožiarov elektrického vedenia,
osvetľovacích rámp, vodiče a laná, výstuže optických a iných káblov, izolátory a pod.
pre tlak). Takto sú namáhané napr. tyče (prúty) stožiarov elektrického vedenia,
osvetľovacích rámp, vodiče a laná, výstuže optických a iných káblov, izolátory a pod.
obr.4.5 Čistý ťah, tlak
 |
O prostom šmyku hovoríme vtedy, ak v myslenom reze pôsobia len
zložky výslednice vnútorných síl Py a Pz
obr.4.6a alebo len jedna z nich. Výsledná šmyková sila v danom reze je daná
vektorovým súčtom obidvoch zložiek. Najjednoduchším prípadom šmykového namáhania je
strihanie materiálu obr.4.6b. Pretože výslednica vnútorných síl leží v myslenom
reze, pri prostom šmyku vzniká šmykové napätie
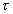 . .
obr.4.6 Čistý šmyk
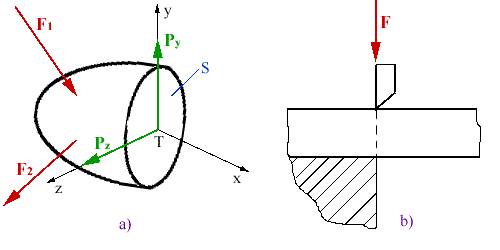 |
O tomto druhu namáhania hovoríme vtedy, ak v myslenom reze zo všetkých
možných zložiek pôsobí len moment Mx = Mk,
ktorého rovina pôsobenia je totožná s rovinou rezu obr.4.7a. Najjednoduchším
prípadom namáhania tohto druhu je krútenie tyče (hriadeľa) kruhového prierezu
obr.4.7b.
obr.4.7 Čistý krut
 |
Krútením sú napr. namáhané hriadele a osi točivých strojov.
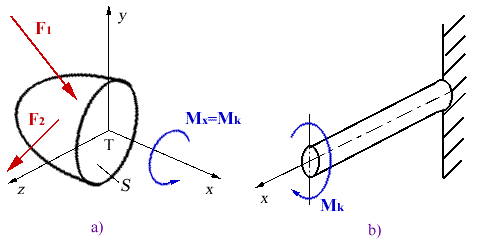
O prostom ohybe hovoríme vtedy, ak v myslenom reze pôsobí len
moment My alebo len Mz obr.4.8a. Ak
pôsobia obidve zložky súčasne, hovoríme spravidla o
šikmom ohybe.
Najjednoduchší prípad tohoto druhu namáhania je znázornený na
obr.4.8b. Konštrukčné prvky prenášajúce ohybový moment nazývame
nosníkmi.
obr.4.8 Čistý ohyb
 |
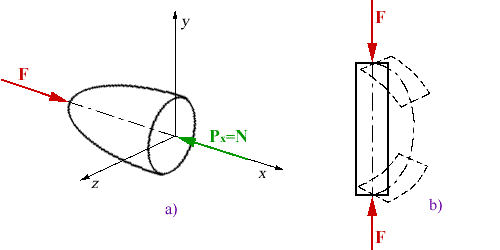
Podobne ako pri prostom tlaku, i v tomto prípade pôsobí v myslenom
reze tlaková sila Px = N obr.4.9a. Ak priečny prierez
tyče je proti jej dĺžke malý (štíhly prút), dôjde po prekročení určitej (kritickej)
hodnoty osovej sily k vybočeniu priamej pozdĺžnej osi prúta, tyč sa prehne, až sa zlomí -
stratí stabilitu obr.4.9b. Stratiť stabilitu môžu konštrukčné prvky
(štíhle, tenkostenné) namáhané tlakovou silou, ako sú napríklad prúty stožiarov, rámp,
veží a anténnych systémov.
obr.4.9 Vzper štíhleho prúta
 |
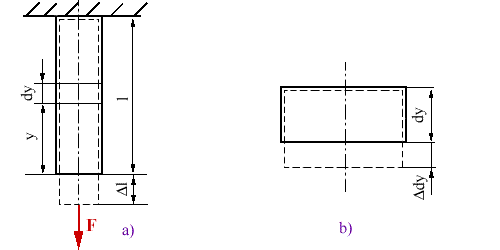
Ak namáhame priamu tyč ťahom podľa obr.4.10b, pozorujeme, že tyč
sa predlžuje a jej prierez sa zužuje. Zúženie prierezu tyče oproti jej predĺženiu býva
zanedbateľné.
obr.4.10 Namáhanie osovou silou F
 |
Dvoma rovnobežnými myslenými rezmi vyberme z tyče valček nekonečne malej
výšky
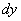 vo vzdialenosti y obr.4.10b od spodného okraja tyče.
Zaťažením tyče sa valček predĺži o hodnotu
vo vzdialenosti y obr.4.10b od spodného okraja tyče.
Zaťažením tyče sa valček predĺži o hodnotu
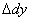 .
.
Pomer
nazývame pomerným predĺžením tyče. Je to
predĺženie pripadajúce na jednotku dĺžky tyče. Ak je pomerné predĺženie vo všetkých bodoch
prierezu a vo všetkých priečnych prierezoch rovnaké, možno celkové predĺženie tyče
vyjadriť vzťahom
odkiaľ
Ako vidieť z týchto rovníc pomerné predĺženie je
veličina bezrozmerná.
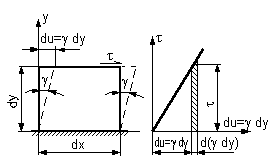
Uvažujeme elementárnu časť plochy prierezu ABCD s rozmermi dx,
dy obr.4.11, ktorá sa vplyvom šmykových napätí
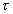 pretvorí, ako je to na obrázku vyznačené.
pretvorí, ako je to na obrázku vyznačené.
obr.4.11 Pomerné skosenie
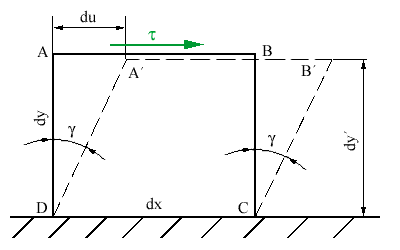 |
Ak je toto pretvorenie malé, môžeme zmenu dĺžky dy zanedbať.
Posunutie du môžeme potom vyjadriť vzťahom
alebo
Keďže uhol
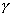 je
malý, možno písať: je
malý, možno písať:
takže bude
a z toho pomer
nazývame pomerným skosením (tiež zmena pravého uhla v elementárnom
hranolčeku). Tak ako pomerné predĺženie, aj táto veličina je bezrozmerná. Pomerné predĺženie
a skosenie sú základnými zložkami deformácie telesa.
Informácie o pružnosti a pevnosti materiálu nám dávajú
skúšky mechanických vlastností. Jedna z takýchto skúšok je trhacia
skúška ťahom. Skúšobná tyč normalizovaného tvaru a rozmerov sa upne do čeľustí trhacieho
stroja a postupne sa plynule zaťažuje prostým ťahom. Pritom sa automaticky zaznamenáva
závislosť medzi zaťažením a príslušným predĺžením skúšobnej tyče. Pri známych rozmeroch
skúšobnej tyče (počiatočný prierez S, dĺžka l) možno získať závislosť
pomerného predĺženia od napätia.
Na obr.4.12 je nakreslený diagram napätia a pomerného
predĺženia "mäkkej" konštrukčnej ocele. Z obrázku vidieť, že časť diagramu
až po bod U je lineárny, čiže napätie je úmerné pomernému predĺženiu. Napätie
prislúchajúce bodu U nazývame medzou úmernosti
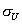 .
Pri skúške možno nájsť také napätie, po hodnotu ktorého bude mať tyč len pružné
deformácie. Toto napätie sa nazýva medza pružnosti .
Pri skúške možno nájsť také napätie, po hodnotu ktorého bude mať tyč len pružné
deformácie. Toto napätie sa nazýva medza pružnosti
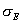 .
Bod E leží spravidla vyššie, ale veľmi blízko k bodu U. Ak skúšobnú tyč odľahčíme v stave pod
medzou pružnosti, pružné (elastické) deformácie vymiznú a skúšobná tyčka nadobudne svoj
pôvodný tvar. Po prekročení medze pružnosti začnú vznikať trvalé-plastické
deformácie. V bode K sa začne skúšobná tyč predlžovať bez toho, že by napätie
stúpalo. Napätie prisluchajúce bodu K (resp. K´) nazývame hornou (resp. spodnou)
medzou klzu. Veľkosť elastoplatických deformácií .
Bod E leží spravidla vyššie, ale veľmi blízko k bodu U. Ak skúšobnú tyč odľahčíme v stave pod
medzou pružnosti, pružné (elastické) deformácie vymiznú a skúšobná tyčka nadobudne svoj
pôvodný tvar. Po prekročení medze pružnosti začnú vznikať trvalé-plastické
deformácie. V bode K sa začne skúšobná tyč predlžovať bez toho, že by napätie
stúpalo. Napätie prisluchajúce bodu K (resp. K´) nazývame hornou (resp. spodnou)
medzou klzu. Veľkosť elastoplatických deformácií
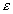 pri dosiahnutí medze klzu pri konštrukčných oceliach neprekračuje hodnotu 0,001 ~ 0,003.
pri dosiahnutí medze klzu pri konštrukčných oceliach neprekračuje hodnotu 0,001 ~ 0,003.
obr.4.12 Skúška v ťahu
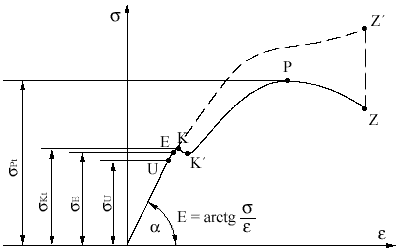 |
Najväčšia hodnota napätia pri skúške je daná napätím
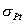 (bod P) - medza pevnosti v ťahu. Konečné porušenie nastáva
však pri napätí, ktoré prislúcha bodu Z. Na obr.4.12 je čiarkovanou čiarou
vyznačený priebeh tej istej závislosti, vzťahovaný však na okamžitý prierez tyčky.
Materiál, pri ktorom nastáva porucha po značných elastoplatických deformáciách, sa
nazýva húževnatý.
(bod P) - medza pevnosti v ťahu. Konečné porušenie nastáva
však pri napätí, ktoré prislúcha bodu Z. Na obr.4.12 je čiarkovanou čiarou
vyznačený priebeh tej istej závislosti, vzťahovaný však na okamžitý prierez tyčky.
Materiál, pri ktorom nastáva porucha po značných elastoplatických deformáciách, sa
nazýva húževnatý.
obr.4.13 Krehký materiál
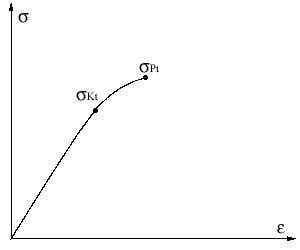 |
Na obr.4.13 je znázornený diagram ťahovej skúšky liatiny. Tento
materiál má veľmi nízku medzu úmernosti a nemá jasne vyhranenú medzu klzu. Medza klzu sa
nachádza blízko medze pevnosti materiálu. Takýto materiál pri ktorom nastane porucha bez
významnejších elastoplatických deformácií, nazývame krehkým.
Skrehnúť môže aj pôvodne húževnatý materiál, napr. vplyvom teplotného
namáhania. Materiál jadrového reaktora krehne aj vplyvom radiačného žiarenia. Typickým
krehkým materiálom je tiež sklo, keramika, a iné.
Lineárnu závislosť medzi napätím a deformáciou do medze úmernosti
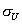 definoval roku 1860 Robert Hooke jedným zo základných zákonov pružnosti a pevnosti:
definoval roku 1860 Robert Hooke jedným zo základných zákonov pružnosti a pevnosti:
ktorý nazývame Hookov zákon.
Konštantu úmernosti E nazývame
modulom pružnosti v ťahu. Modul pružnosti charakterizuje
mechanickú vlastnosť - pružnosť materiálu a je závislý od druhu materiálu skúšobnej
tyčky. Pretože pomerné predĺženie
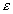 je bezrozmerná veličina, má modul pružnosti v ťahu rozmer napätia, teda
je bezrozmerná veličina, má modul pružnosti v ťahu rozmer napätia, teda
Pre oceľ nadobúda hodnoty
E = 2,1.105 N.mm-2. Hliník má modul pružnosti
78000 MPa, sklenná výstuž optických vlákien má E = 50000 MPa.
Modul pružnosti rôznych materiálov je závislý na technológií výroby a jeho
ďalšom spracovaní.
Ak namáhame nejakú látku prostým šmykom, možno skúškami určiť vzťah medzi
šmykovým napätím
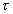 a
pomerným skosením a
pomerným skosením
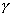 . Na
obr.4.14 je nakreslený diagram konštrukčnej ocele, ktorý sa zistil pri namáhaní
tenkostennej rúrky prostým krútením. . Na
obr.4.14 je nakreslený diagram konštrukčnej ocele, ktorý sa zistil pri namáhaní
tenkostennej rúrky prostým krútením.
obr.4.14 Závislosť medzi šmykovým napätím a pomerným
skosením
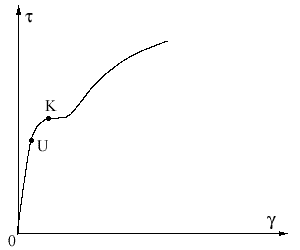 |
Diagram sa podobá diagramu skúšok v ťahu a možno na ňom vidieť medzu
úmernosti
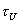 (bod U) a medzou klzu
(bod U) a medzou klzu
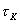 (bod K). Po medzu úmernosti platí vzťah
(bod K). Po medzu úmernosti platí vzťah
Kde G je materiálová konštanta a nazýva sa
modul pružnosti v šmyku. Pretože
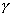 je
bezrozmerná veličina, má i tento modul (tak ako aj E) rozmer napätia. Hodnota
modulu pružnosti v šmyku pre oceľ je
G = 0,8.105 N.mm-2 = 0,8.1011
N.m-2 je
bezrozmerná veličina, má i tento modul (tak ako aj E) rozmer napätia. Hodnota
modulu pružnosti v šmyku pre oceľ je
G = 0,8.105 N.mm-2 = 0,8.1011
N.m-2
Ak je modul pružnosti materiálu vo všetkých smeroch rovnaký, hovoríme, že
látka je izotropná. Materiály používané v konštrukčnej praxi
považujeme spravidla za izotropné a
homogénne, t.j. také, ktoré majú vo všetkých smeroch rovnaké
materiálové vlastnosti. V opačnom prípade hovoríme o
anizotropných látkach. Modul pružnosti ako aj iné vlastnosti
materiálov možno nájsť na web stránke
www.mems.org.
Súčasne s predĺžením skúšobnej tyče v smere pozdĺžnej osi pozorujeme pri
prostom ťahu aj skrátenie jej priečnych rozmerov. Toto skrátenie je, ako ukázali
skúšky, v rozsahu platnosti Hookovho zákona pri izotropných materiáloch úmerne napätiu
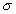 , a tým i
osovému pomernému predĺženiu , a tým i
osovému pomernému predĺženiu
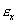 .
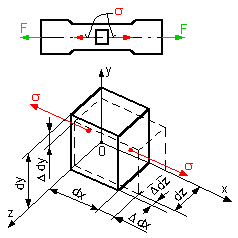
Keď vytkneme zo skúšobnej tyče elementárny hranolček podľa obr. 4.15, potom možno priečne
zúženia v smere y a z popísať rovnicami: .
Keď vytkneme zo skúšobnej tyče elementárny hranolček podľa obr. 4.15, potom možno priečne
zúženia v smere y a z popísať rovnicami:
Súčiniteľa m nazývame Poissonova konštanta.
Často, najmä v numerických metódach, sa používa jej prevrátená hodnota, ktorú nazývame
Poissonovým číslom. Pre oceľ je Poissonova konštanta
resp. Poissonovo číslo
obr.4.15 Deformácia pri jednoosovej napätosti
 |
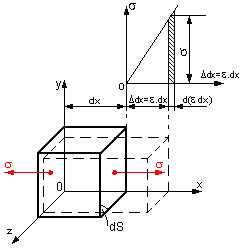
obr.4.16 Energia napätosti normálových napätí
 |
Energiou napätosti rozumieme energiu, ktorá sa skumuluje v pôvodne
nezaťaženom telese, keď nadobudne určité pretvorenie, a to od všetkých vnútorných síl
pôsobiacich na nekonečne malé elementy telesa. Táto energia - za predpokladu platnosti
Hookovho zákona - sa rovná práci vonkajších síl, vykonanou pri pretvorení telesa. Vonkajšie a
vnútorné sily musia byť pritom v statickej rovnováhe.
Deformačnú prácu vonkajších síl - podľa definície známej z fyziky - určíme
podľa vzťahu
Kde F je zaťažujúca sila, ktorá pôsobí na dráhe s. Energiu
napätosti určíme osobitne pre normálové a osobitne pre šmykové napätia, pričom využijeme
horeuvedený vzťah.
a) Energia napätosti normálových napätí
Pri namáhaní normálovým napätím v smere osi x vzniká deformácia
elementárneho hranola podľa obr. 4.16. Za predpokladu platnosti Hookovho zákona je závislosť
medzi napätím
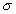 a
pretvorením a
pretvorením
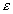 lineárna.
lineárna.
Vnútorná sila pôsobiaca na plochu dS elementárneho hranolčeka bude
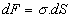 . Potom
elementárna deformačná práca . Potom
elementárna deformačná práca
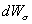 ,
ktorá je rovná energii napätosti ,
ktorá je rovná energii napätosti
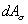 elementárneho hranolčeka, bude
elementárneho hranolčeka, bude
Pretože
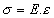 a dx, dy a dz sú konštanty, možno túto rovnicu upraviť do tvaru
a dx, dy a dz sú konštanty, možno túto rovnicu upraviť do tvaru
kde dV = dx dy dz je objem elementu. Celková energia napätosti
potom bude
Poznámka: Energia napätosti
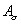 je vždy kladná, i keď pôjde o namáhanie v tlaku. Vtedy
je vždy kladná, i keď pôjde o namáhanie v tlaku. Vtedy
b) Energia napätosti šmykových napätí
Podobne ako pri normálových napätiach, možno vyjadriť energiu napätosti
šmykových napätí (obr. 4.17)
obr.4.17 Energia napätosti šmykových napätí
 |
Celková energia napätosti v danom telese je vo všeobecnom prípade daná súčtom
energie napätosti normálových a šmykových napätí
Uvažujeme poddajné teleso, ktoré je zaťažené rovnovážnou silovou sústavou
F1, F2, ....,Fi,
....,Fn (obr. 4.18).
obr.4.18 Castiglianova veta
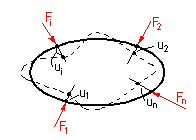 |
Pôsobiská vonkajších síl sú na povrchu telesa, ktoré sa pri pretvorení telesa
posunú o hodnoty u1, u2, ....,ui,
....,un. Pretože napätia
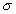 a a
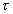 sú v konečnom dôsledku pre teleso daných rozmerov funkciou zaťažujúcich síl, bude aj celková
energia napätosti funkciou síl A = f(F1, F2,
....,Fi, ....,Fn). Ak zväčšíme napr. silu
F1 o veľmi malú hodnotu dFi , zväčší sa posunutie o
dui a energia napätosti o hodnotu
sú v konečnom dôsledku pre teleso daných rozmerov funkciou zaťažujúcich síl, bude aj celková
energia napätosti funkciou síl A = f(F1, F2,
....,Fi, ....,Fn). Ak zväčšíme napr. silu
F1 o veľmi malú hodnotu dFi , zväčší sa posunutie o
dui a energia napätosti o hodnotu
takže energia napätosti bude
kde A je práca sily Fi na posunutiach
(ui + dui), a súčin dvoch malých veličín
dFi.dui zanedbáme. Potom
resp.
Výsledná rovnica je matematickým vyjadrením prvej Castiglianovej vety, podľa
ktorej posunutie pôsobiska ľubovoľnej sily pri deformácii telesa (za predpokladu platnosti
Hookovho zákona) sa rovná parciálnej derivácii celkovej energie napätosti podľa tejto sily.
Zmysel posunutia sily ui súhlasí so zmyslom sily Fi.
Poznámka: I. Castiglianova veta vyžaduje taktiež
platnost zákona superpozície účinkov, ktorý si vysvetlíme
neskôr. Zákon superpozície účinkov hovorí: Ak na teleso pôsobí sústava
vonkajších síl, potom výsledný napäťový a deformačný účinok je rovný súčtu účinkov od
jednotlivých síl, pričom nezáleží na poradí pôsobiacich síl.
Pri odvádzaní tejto vety mohli sme však znakom Fi označiť
aj moment točivej dvojice síl Mi a znakom ui zase
príslušné natočenie
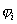 (obr. 4.19).
(obr. 4.19).
obr.4.19 Uhol natočenia
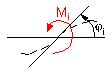 |
Postup i výsledok by boli rovnaké a preto možno tiež písať:
I.Castiglianovu vetu budeme používať na vyjadrenie deformácie telesa.
Trhacia skúška nám dáva dôležité údaje o mechanických vlastnostiach
materiálu. Ak z nej poznáme medzu klzu a medzu pevnosti materiálu, môžeme určiť pre každú
technickú úlohu veľkosť napätia, ktoré môžeme pokladať za bezpečné. Toto prípustné napätie
voláme dovoleným namáhaním. Pri voľbe dovoleného namáhania pre
oceľ si treba uvedomiť, že tento materiál pri napätiach pod medzou úmernosti môžeme považovať za
dokonale pružný a pri napätiach nad touto medzou dochádza k trvalému plastickému pretvoreniu.
Ak chceme pripustiť len pružné deformácie, dovolené namáhanie musí byť nižšie ako je medza
úmernosti daného materiálu. Pretože zisťovanie tejto medze je dosť obtiažne a jej poloha závisí
od presnosti merania, berieme pre určenie dovoleného namáhania materiálu obyčajne medzu klzu alebo
medzu pevnosti. Veľkosť dovoleného namáhania potom určujeme podľa rovníc:
kde sk, resp. sp sú miery bezpečnosti
vzhľadom na medzu klzu
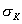 , resp.
na medzu pevnosti , resp.
na medzu pevnosti
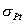 . .
Pri konštrukčných oceliach berieme obvykle za základ pre výpočet dovoleného
namáhania medzu klzu
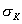 .
Pri statickom namáhaní pritom uvažujeme mieru bezpečnosti sk .
Pri statickom namáhaní pritom uvažujeme mieru bezpečnosti sk
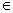 (1,4~1,6). Pre krehké materiály (liatinu a pod.) berieme za základ na určenie dovoleného
namáhania medzu pevnosti
(1,4~1,6). Pre krehké materiály (liatinu a pod.) berieme za základ na určenie dovoleného
namáhania medzu pevnosti
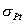 .
Mieru bezpečnosti volíme v závislosti od presnosti zvoleného matematického modelu danej
konštrukcie, ako aj metódy riešenia homogenity použitých látok. .
Mieru bezpečnosti volíme v závislosti od presnosti zvoleného matematického modelu danej
konštrukcie, ako aj metódy riešenia homogenity použitých látok.
Pre mnohé konštrukcie sú
hodnoty miery bezpečnosti určené normamy STN.
Podľa rovnakých metód volíme dovolené namáhanie v šmyku:
Ako uvidíme ďalej, je vzájomný vzťah medzi
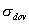 a a
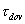 určených hypotézami pevnosti. Je zrejmé, že ak súčiastka má pracovať s príslušnou
bezpečnosťou, musí byť splnená bezpečnostná podmienka
určených hypotézami pevnosti. Je zrejmé, že ak súčiastka má pracovať s príslušnou
bezpečnosťou, musí byť splnená bezpečnostná podmienka
alebo
kde
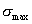 a
a 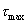 sú maximálne hodnoty napätia.
sú maximálne hodnoty napätia.
|

 Výučba
Mechaniky
Výučba
Mechaniky