|
Učebný cieľ kapitoly
Po preštudovaní tejto kapitoly by ste mali ovládať:
- Kedy nastáva namáhanie na čistý ťah-tlak
- Ktorá zložka výslednice vnútorných síl je nenulová
- Ako je definované normálové napätie čistého ťahu-tlaku
- Podľa akého pravidla volíme myslené rezy
- Načo určujeme priebeh osových síl a normálových napätí
- Ako sa vypočíta celkové predĺženie (skrátenie) tyče
- Ako zohľadniť vlastnú tiaž pri výpočte vnútorných síl a celkového predĺženia
- Akým postupom treba riešiť staticky neurčité úlohy
- Ako sa dimenzujú jednoduché prútovky
- Ako sa určí posunutie styčníkov prútovky
- Ako sa riešia staticky neurčité prútovky
- Ako sa vykonáva statická analýza zložitých prútoviek
- Ako je definovaná tiažová reťazovka - predpoklady a mechanický model
- Aký priebeh má osová sila a normálové napätie po dĺžke reťazovky
- Ako sa určí celkové predĺženie reťazovky
- Ako sa vykonáva statická analýza reťazoviek symetrických a s prevýšením upevnenia jej
koncov
Ak možno určiť výslednicu vnútorných síl - osovú silu
zo statických podmienok rovnováhy, hovoríme o staticky určitej úlohe čistého ťahu alebo tlaku. V
opačnom prípade musíme statické podmienky rovnováhy doplniť ďalšími -
deformačnými podmienkami a hovoríme o staticky neurčitých úlohách.
Medzi prípady namáhania prostým ťahom možno zaradiť: namáhanie vonkajšou osovou silou, vlastnou
tiažou a odstredivou silou a iné.
a) Staticky určité úlohy
Uvažujeme tyč konštatného prierezu na jednom konci pevne zachytenú a na druhom
konci zaťaženú vonkajšou osovou silou F. Zaujíma nás poloha nebezpečného prierezu tyče a
celková deformácia tyče. Na to potrebujeme určiť priebeh výslednice vnútorných síl - osovú silu
N a priebeh normálových napätí
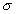 v jednotlivých
myslených rezoch tyče, ako aj celkové predĺženie tyče v jednotlivých
myslených rezoch tyče, ako aj celkové predĺženie tyče
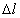 , resp.
pomerné predĺženie , resp.
pomerné predĺženie
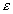 . .
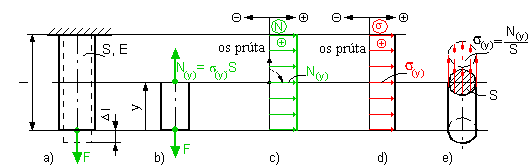
obr.5.1 Čistý ťah
|
Rozrežeme tyč na obr. 5.1a mysleným rezom kolmým na os tyče na dve časti. Počiatok
súradnice y volíme vo voľnom konci tyče. Odrezanú časť tyče 5.1b uvedieme do statickej
rovnováhy tak, že do mysleného rezu vložíme (v kladnom smere - von z rezu) výslednicu vnútorných síl
N(y). Táto osová sila musí byť v rovnováhe s vonkajšími silami pôsobiacimi na odrezanú
časť.
Zo statických podmienok rovnováhy síl do osi y pre odrezanú časť tyče
máme:
V tomto prípade je priebeh N(y) konštatný po celej dĺžke tyče a je nakreslený
na obr. 5.1c.
Z výslednice vnútorných síl možno určiť napätie
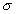 (y) v
jednotlivých myslených rezoch. Pri prútoch s konštatným prierezom alebo prútoch, ktorých prierez sa
málo mení, sila F predlžuje tyč tak, aby sledovaný (pôvodne rovinný prierez) zostal rovinným
aj po deformácii. Z podmienky zachovania rovinnosti prierezu vyplýva, že napätie má konštantnú
hodnotu v každom bode prierezu (obr. 5.1c) a jeho veľkosť bude (y) v
jednotlivých myslených rezoch. Pri prútoch s konštatným prierezom alebo prútoch, ktorých prierez sa
málo mení, sila F predlžuje tyč tak, aby sledovaný (pôvodne rovinný prierez) zostal rovinným
aj po deformácii. Z podmienky zachovania rovinnosti prierezu vyplýva, že napätie má konštantnú
hodnotu v každom bode prierezu (obr. 5.1c) a jeho veľkosť bude
Jeho priebeh v rezoch po dĺžke tyče je znázornený na obr. 5.1b .
Ako vidieť z
priebehov 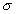 (y) a N(y) (spôsob ich grafického znázorňovania je zrejmý z
obr. 5.1c, d), napätie a osová sila nie je závislá od y. Ako uvidíme neskôr, situácia sa
zmení, ak budeme uvažovať aj pôsobenie objemových síl - vlastnej tiaže telesa. Pre tyč podľa obr.
5.1 je nebezpečným prierezom ľubovoľný rez kolmý na os prúta. (y) a N(y) (spôsob ich grafického znázorňovania je zrejmý z
obr. 5.1c, d), napätie a osová sila nie je závislá od y. Ako uvidíme neskôr, situácia sa
zmení, ak budeme uvažovať aj pôsobenie objemových síl - vlastnej tiaže telesa. Pre tyč podľa obr.
5.1 je nebezpečným prierezom ľubovoľný rez kolmý na os prúta.
Deformáciu tyče - jej celkové predĺženie možno určiť z definície pomerného
predĺženia alebo pomocou I. Castiglianovej vety.
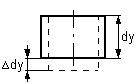
obr.5.2 Pomerné predĺženie
|
Predĺženie elementu dy (obr. 5.2) vyňatej z ťahanej tyče bude
Celkové predĺženie potom bude
Podľa I. Castiglianovej vety určíme posunutie pôsobiska sily F zo vzťahu
resp.
čo súhlasí s výsledkom získaným z definičného vzťahu pre celkové predĺženie.
Priebeh napätia a celkové predĺženie tyče zaťaženej sústavou osových síl možno určiť obdobným
spôsobom.
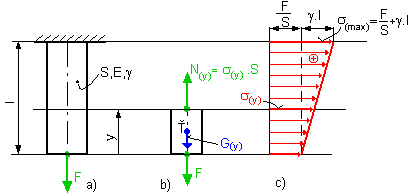
Uvažujeme tyč vo zvislej polohe, ktorej rozmery a v ich dôsledku vlastná tiaž nie je
zanedbateľná voči veľkosti osovej sily F (obr. 5.3). Priebeh napätia určíme opäť metódou
mysleného rezu.
obr.5.3 Vplyv vlastnej tiaže
|
Z podmienok rovnováhy odrezanej časti tyče (obr. 5.3b) dostaneme:
kde G(y) je vlastná tiaž odrezanej časti tyče (
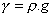 je merná
tiaž). V našom prípade je merná
tiaž). V našom prípade 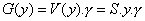 . Potom napätie v myslenom reze je: . Potom napätie v myslenom reze je:
Priebeh
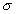 (y)
určíme ako priebeh rovnice priamky v intervale y (y)
určíme ako priebeh rovnice priamky v intervale y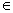 (0, l). (0, l).
Priebeh napätia po dĺžke tyče je znázornený na obr. 5.3c. Nebezpečný prierez sa
nachádza v mieste maximálneho napätia
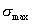 - v
mieste votknutia tyče. Aby nedošlo k porušeniu tyče v nebezpečnom priereze, musí byť splnená
pevnostná podmienka - v
mieste votknutia tyče. Aby nedošlo k porušeniu tyče v nebezpečnom priereze, musí byť splnená
pevnostná podmienka
Celková energia napätosti tyče je
Po dosadení dostaneme:
potom celkové predĺženie tyče
Ten istý výsledok by sme pre celkové predĺženie dostali aj zo vzťahu
Z týchto vzťahov je zrejmé, že napätie, resp. celkové predĺženie tyče je rovné
súčtu napätí, resp. predĺžení, od osovej sily a vlastnej tiaže, čo je vlastne potvrdením
zákona superpozície účinkov. Staticky určité
úlohy namáhania osovou silou riešime podľa postupu uvedeného v príkladoch uvedených v tejto
kapitole.
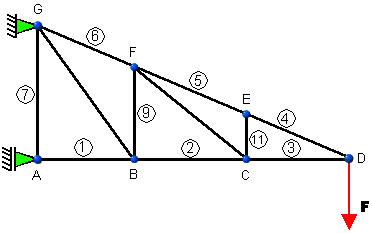
Na obr. 5.4 je znázornené rameno stožiara vysokého napätia. Konštrukčné prvky
označené číslicami 1, 2, …, 11 nazývame prútmi. Prúty sú navzájom
pospájané v bodoch A, B, …, G, ktoré nazývame styčníkmi. Ak
predpokladáme, že prúty sú dostatočne štíhle (rozmery prierezu prúta sú malé oproti jeho dĺžke) a v
styčníkoch sú pospájané v kĺboch bez trenia, možno takúto sústavu priamych prútov považovať za
prútovú sústavu. Pretože ideálne kĺby bez trenia neprenášajú do prútov
žiadne momenty vonkajších síl, prúty sú namáhané len osovými silami. Skutočné koštrukcie (stožiara
vn, osvetľovacie veže, anténne sústavy, …) sú však spájané spravidla zváraním, skrutkovými spojmi a
ideálnej prútovej sústave sa viac-menej len približujú. Toto priblíženie bude tým korektnejšie, čím
sú prúty štíhlejšie a spojenie styčných bodov je menej tuhé. V opačnom prípade treba uvažovať, že
konštrukcia pozostáva z nosníkov.
obr.5.4 Rameno stožiara
|
Pri pevnostnom a tuhostnom návrhu prútových konštrukcií nás zaujíma:
- veľkosť osových síl v prútoch - Pi (i = 1, …, n - číslo prúta)
- celkové predĺženie, resp. skrátenie prútov -
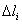
- posunutie styčníkov po zaťažení prútovej sústavy
Používajú sa pritom klasické metódy statiky (styčníková, priesečná, …), ktoré sú
však čoraz viac nahrádzané numerickými metódami (napr. metóda konečných prvkov). Potom nám klasické
metódy slúžia na orientačnú kontrolu správnosti numerického riešenia.
Ak je prútová sústava staticky určitá, na výpočet osových síl stačia klasické
vektorové metódy statiky. Pri staticky neurčitých úlohách musíme vziať do úvahy pri výpočte osových
síl aj deformačné podmienky. V prípade metódy konečných prvkov do určitej miery odpadajú ťažkosti
spojené s návrhom staticky neurčitej prútovej sústavy. Táto metóda riešenia však vyžaduje, aby
vnútorná statická určitosť bola
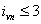 (prútovka a ani
jej časť nesmie byť mechanizmom). (prútovka a ani
jej časť nesmie byť mechanizmom).
a) Jednoduché prútové sústavy
a1) Staticky určité
úlohy
Sily v jednotlivých prútoch staticky určitej prútovej sústavy určíme z rovnováhy
uvoľnených styčníkov, pričom účinok prútov nahradíme osovými silami. Ak poznáme osové sily v
jednotlivých prútoch, môžeme určiť predĺženia, resp. skrátenia prútov.
Priklad 1
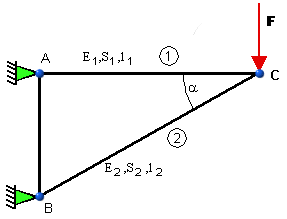
Určite osové sily v prútoch 1 a 2, zvislé a vodorovné posunutia
styčníka C prútovej sústavy (obr. 5.5) zaťaženej silou F, ak vlastnú tiaž prútov
neuvažujeme.
obr.5.5 Prútovka
|
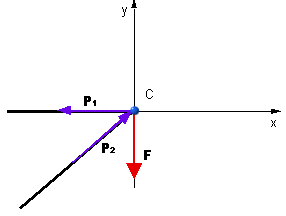
obr.5.6 Rovnováha styčníka
|
Uvoľníme styčník C a vložíme do neho v predpokladanom smere pôsobenia osové
sily (tlaková sila smeruje do styčníka, ťahová sila smeruje von zo styčníka) P1 a
P2 (obr. 5.6).
Zo statických podmienok rovnováhy dostaneme:
Osové sily vyšli so znamienkom +, preto podľa úvodného predpokladu v prúte číslo
1 je ťah a v prúte č. 2 je tlak.
Posunutie styčníka určíme z predĺženia, resp. skrátenia prútov 1 a 2. Predĺženia
prútov sú:
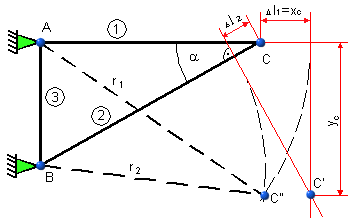
obr.5.7 Posunutie styčníka
|
Na určenie pretvorenia sústavy stačí opísať kružnice z bodov A a B (obr. 5.7) s
polomermi:
Keďže deformácie musia byť malé, možno kružnice nahradiť dotyčnicami kolmými na
prúty nedeformovanej sústavy (obr. 5.7, 5.8).
Potom vodorovné posunutie
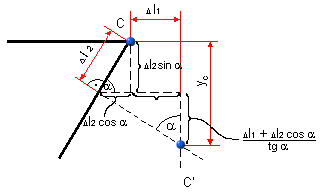
Zvislé posunutie vypočítame z geometrických závislostí vo zväčšenej mierke
nakresleného štvoruholníka.
obr.5.8 Geometrická závislosť
|
Zvislé posunutie bude:
Priklad 2
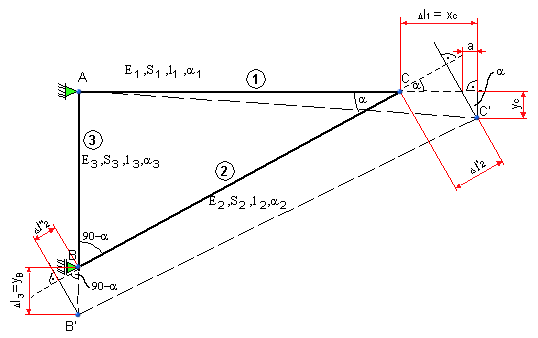
Určite sily v prútoch prútovej sústavy podľa obr. 5.9, ako aj vodorovné a zvislé
posunutie styčníkov C a B, ak všetky prúty zohrejeme o rovnaký teplotný rozdiel z teploty
t0 na teplotu t.
Zo statických podmienok rovnováhy uvoľnených styčníkov zistíme, že osové sily v
prútoch sú nulové. (Ak zohrejeme prúty staticky určitej prútovej
sústavy o rovnaký teplotný rozdiel, osové sily od teplotného zaťaženia sú rovné nule. Pre
staticky neurčité prútové sústavy to však neplatí). Posunutie styčníkov je dané predĺžením
jednotlivých prútov vplyvom teplotnej rozťažnosti:
Posunutie styčníka C:
Posunutie styčníka B:
pričom
obr.5.9 Posunutie styčníkov
|
a2) Staticky neurčité
úlohy
Jednoduché prútové sústavy, pri ktorých nemožno určiť osové sily v prútoch len zo
statických podmienok rovnováhy, nazývame staticky neurčitými. V tomto prípade musíme statické
podmienky rovnováhy styčníka doplniť deformačnými podmienkami (musí byť zohľadnená podmienka
neporušenosti spojenia prútov v styčníkoch po deformácii). Celkový počet rovníc musí byť totožný s
celkovým počtom neznámych osových síl v styčníku.
Priklad 1
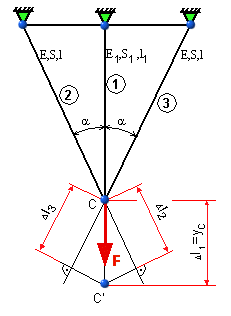
Stanovte sily v prútoch sústavy podľa obr. 5.10 zaťaženej silou F.
Z
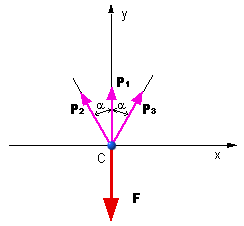
podmienok rovnováhy uvoľneného styčníka (obr. 5.11) máme:
Pretože máme tri neznáme sily, musíme napísať tretiu, doplňujúcu rovnicu. Z
posunutia styčníka C (obr. 5.10) vidíme, že
Dosadením za P1 z rovnice 1. do rovnice 3. máme:
resp.
Osové sily vyšli so znamienkom +, to znamená, že pôsobia v smere zvolenom na
obr.5.11. Vo všetkých troch prútoch je ťah. Pevnostná podmienka pre návrh prútov bude
kde index i označuje číslo prúta.
obr.5.10 Staticky neurčitá úloha
|
obr.5.11 Uvoľnený styčník
|
Príklad 2
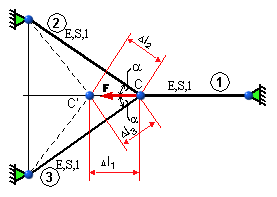
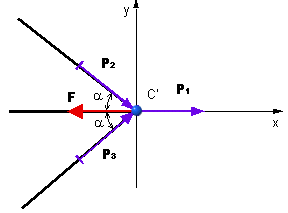
Určite osové sily prútovej sústavy podľa obr. 5.12 zaťaženej silou F.
obr.5.12 Posunutie styčníka
|
Z rovnováhy uvoľneného C styčníka máme (obr. 5.11):
Dosadením do rovnice 1. máme:
V tejto rovnici sú dve neznáme, preto napíšeme deformačnú podmienku, ktorá vyplýva
z celkových predĺžení, resp. skrátení prútov:
obr.5.13 Rovnováha styčníka
|
Pre posunutie styčníka C teda platí:
Odtiaľ
a po úprave
Osové sily vyšli so znamienkom +, to znamená, že pôsobia v tom zmysle, ako
sme ich zakreslili na obr. 5.13. V prúte 1 je ťah, v prútoch 2 a 3 je
tlak.
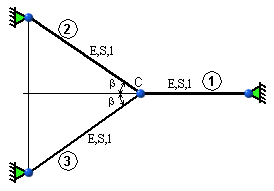
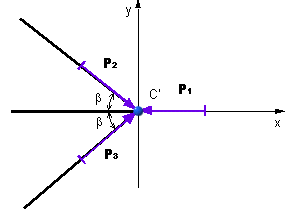
Príklad 3
Určite sily v prútoch prútovej sústavy podľa obr. 5.14, ak prút č. 1 bol ohriaty o teplotný
rozdiel 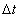 .
Teplotná rozťažnosť materiálu je .
Teplotná rozťažnosť materiálu je 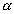 . .
Z rovnováhy uvoľneného styčníka máme (obr. 5.13):
Z rovnice 1. dostaneme
obr.5.14 Prútová sústava
|
obr.5.15 Uvoľnený styčník
|
Na výpočet troch neznámych síl musíme podmienky rovnováhy doplniť deformačnou
podmienkou. Predĺženia prútov sú:
Posunutie styčníka zistíme z tejto úvahy:
Keby prút 1 bol uložený voľne v priestore, vplyvom ohriatia by sa predĺžil o hodnotu
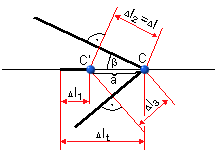
Vo voľnej deformácii mu však bránia prúty 2 a 3. Bude v ňom pritom
vznikať tlaková sila, ktorá zníži veľkosť teplotného predĺženia 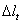 o hodnotu o hodnotu
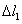 (Obr. 5.16).
(Obr. 5.16).
obr.5.16 Skrátenie prúta
|
Potom
Dosadením za P1 do rovnice 3. a po úpravách dostaneme:
Veľkosť osových síl je priamo úmerná veľkosti teplotného rozdielu. Treba upozorniť,
že pri staticky neurčitých prútovkách vnikajú značné osové sily už pri relatívne malých teplotných
rozdieloch  . .
Príklad 4
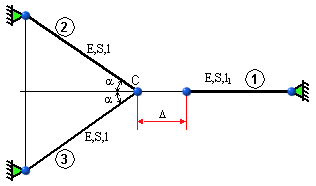
Určite sily v prútoch, ak prút č. 1 bol vyrobený o hodnotu  kratší (obr. 5.17).
Z obr. 5.17 je zrejmé, že spojenie prútov v spoločnom styčníku musí byť násilné. Prút č. 1
sa musí predĺžiť o hodnotu kratší (obr. 5.17).
Z obr. 5.17 je zrejmé, že spojenie prútov v spoločnom styčníku musí byť násilné. Prút č. 1
sa musí predĺžiť o hodnotu
a prúty 2 a 3 o hodnotu
obr.5.17 Vplyv výrobnej nepresnosti
|
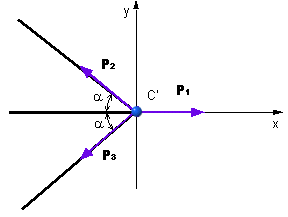
Sily P1 a P2 = P3 = P
sú zakreslené v styčníku C a z jeho rovnováhy vyplýva (obr. 5.18):
obr.5.18 Rovnováha styčníka
|
Rovnice rovnováhy doplníme deformačnou podmienkou, ktorá vyplýva z obr. 5.19.
Potom
5.19 Poloha styčníka

|
Dosadením za P1 a po úpravách dostaneme:
Ako vidíme, veľkosť osových síl je priamo úmerná veľkosti nepresnosti
 . .
Poznámka: Ak je prútovka namáhaná súčasne vonkajšími silami, teplotou,
prípadne aj prúty sú vyrobené nepresne, výsledné osové sily budú dané superpozíciou osových síl od
jednotlivých prípadov zaťaženia.
b) Zložité prútové sústavy
b1) Staticky určité úlohy
Rovinná prútová sústava je staticky určitá, keď ivo = 0,
ivn = 3. Osové sily v prútoch určíme klasickými metódami statiky (styčníková,
priesečná, princíp virtuálnych prác, a iné). Vzhľadom na prácnosť ich aplikácie pri prútovkách s
veľkým počtom prútov, ich hlavné využitie je na kontrolu výsledkov riešenia dosiahnutých
numerickými metódami, napr. metódou konečných prvkov.
Priklad 1
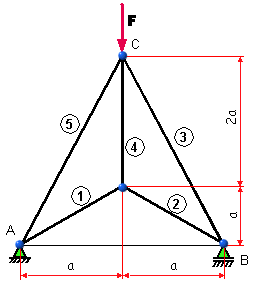
Pre prútovú sústavu podľa obr. 5.20
určite:
- statickú určitosť
- osové sily v prútoch
- prierezy prútov tak, aby
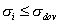
- posunutia styčníka C
obr.5.20 Zadanie úlohy
|
a) Statická určitosť
Vonkajšia statická
určitosť (väzby A a B odoberajú tri stupne voľnosti) je
Vnútorná statická určitosť
prútová sústava je staticky určitá.
b) Osové sily
Na výpočet osových síl použijeme
styčníkovú metódu. Pre riešenie rovnováhy styčníka A a B musíme určiť väzbové reakcie. Väzbové
reakcie RAX, RAY a RB musia byť v statickej
rovnováhe so zaťažujúcou silou F (obr. 5.21).
Vzhľadom na symetriu úlohy
obr.5.21 Väzbové reakcie

|
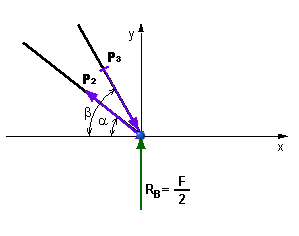
Rovnováha styčníka B
5.22 Rovnováha styčníka B
|
Z dvoch rovníc o dvoch neznámych možno určiť osové sily:
V prúte 2 je ťah a v prúte 3 je tlak. Vzhľadom na symetriu úlohy
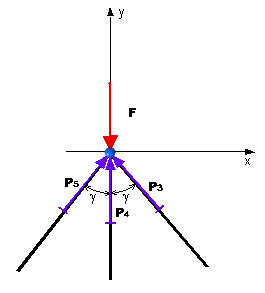
možno predpokladať, že P2 = P1, P3 =
P5. Silu v prúte 4 určíme z rovnováhy styčníka (obr. 5.23):
5.23 Rovnováha styčníka C
|
c) Prierezy prútov
Prierezy prútov určíme z
pevnostnej podmienky 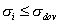 : :
d) Posunutie styčníka C
Bod C sa posunie v zvislom
smere o hodnotu xC, ktorá podľa I. Castiglianovej vety bude
pričom celková energia napätosti prútovej sústavy bude rovná súčtu energií
napätosti jednotlivých prútov namáhaných čistým ťahom, resp. tlakom
Potom
Kde 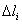 sú predĺženia, resp. skrátenia i-teho prúta a sú predĺženia, resp. skrátenia i-teho prúta a 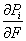 je parciálna derivácia
osovej sily v i-tom prúte podľa sily F. Ei a Si je modul
pružnosti v ťahu, resp. prierez i-tého prúta. je parciálna derivácia
osovej sily v i-tom prúte podľa sily F. Ei a Si je modul
pružnosti v ťahu, resp. prierez i-tého prúta.
Priklad 2
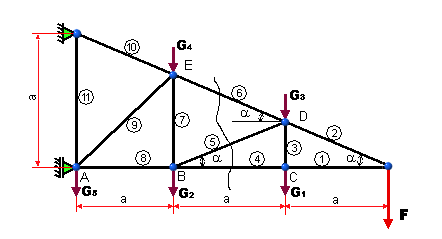
Rameno stožiara vysokého napätia je
zaťažené tiažou vodiča F a vlastnou tiažou prútov, ktorá je rozdelená do styčníkov A, B, C,
D a E (obr. 5.24). Určite osové sily v prútoch 4, 5 a 6 priesečnu metódou.
Výpočet má slúžiť ako kontrola numerického riešenia.
5.24 Zadanie úlohy
|
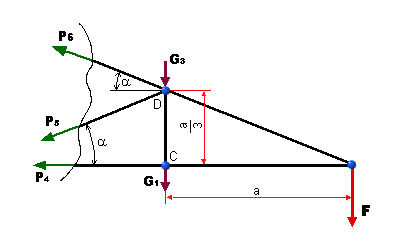
Ako možno výpočtom zistiť, prútová sústava je staticky určitá. Osové sily v prútoch
4, 5 a 6 určíme tak, že rozrežeme rameno mysleným rezom na dve polovice a
riešime rovnováhu odrezanej časti (obr. 5.25):
5.25 Rovnováha odrezanej časti ramena
|
Riešením rovníc 1 a 2 máme:
odkiaľ
b2) Staticky neurčité úlohy
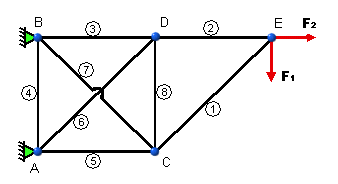
Uvažujme prútovú
sústavu podľa obr. 5.26. Ako vidieť, prútová sústava je tak po vonkajšej, ako aj po vnútornej
stránke staticky neurčitá:
5.26 Zadanie úlohy
|
Prútová sústava je raz po vonkajšej stránke staticky neurčitá a raz vnútorne
staticky neurčitá. Na výpočet osových síl treba doplniť statické podmienky rovnováhy dvoma
deformačnými podmienkami. Obvykle sa takéto prútovky riešia Castiglianovou vetou. Najvýhodnejšie je
však použiť numerické metódy, a preto sa v tomto texte nebudeme zaoberať analytickým riešením
staticky neurčitých prútových sústav. Podstata pevnostného a tuhostného návrhu staticky neurčitých
prútových sústav je rovnaká ako pri staticky určitých úlohách. Staticky neurčité prútové sústavy sú
z hľadiska pevnosti a tuhosti často výhodnejšie konštrukcie, zložitejšia je však ich statická
analýza pôvodnými analytickými metódami. Preto prevládalo v minulosti úsilie navrhovať sústavy
staticky určité. S rozvojom numerických metód však tento problém odpadá.
Pri rozvode elektrickej energie ako aj v bežnej technickej praxi sa stretávame s
prvkami namáhanými na ťah, ktorý je spôsobený najmä vlastnou tiažou. Tieto prvky ako
sú napríklad vodiče napätia, nosné laná a pod., možno považovať za dokonale ohybné vlákna
konštantného prierezu zaťažené vlastnou tiažou samotného vlákna, ako aj dodatočným po dĺžke
vlákna rovnomerne rozloženým spojitým zaťažením q (napr. tiaž námrazy). Takéto vlákno
nie je schopné prenášať ohybový moment, a bude prenášať len čistý ťah.
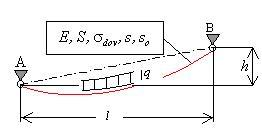
obr.5.27 Ťiažová reťazovka
|
Vlákno (reťazovka) je uchytená v bodoch A a B, ktorých rozpätie je l a
prevýšenie upevnenia je h. Ak pôvodná (priama) dĺžka vlákna bola s0,
po jej zavesení vplyvom vertikálne pôsobiacej tiaže sa ustáli v deformovanom tvare s novou
dĺžkou vlákna s (obr.5.27). Ak je priehyb vlákna proti rozpätiu malý, potom rozdiel
medzi dĺžkou s a dĺžkou priamej spojnice bodov A a B je malý. Ak uvedený rozdiel je menší
ako 10%, možno s dostatočnou presnosťou predpokladať, že tiaž vlákna, eventuálne námrazy, je
rovnomerne rozložená po dĺžke priemetu vlákna do vodorovnej osi a nie po dĺžke krivky. Materiál
vlákna je definovaný modulom pružnosti E, pričom dovolené namáhanie vlákna je
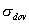 ,
a prierez vlákna je S. ,
a prierez vlákna je S.
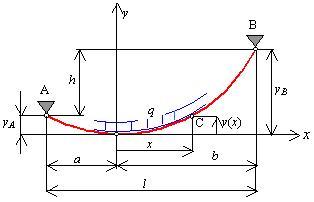
Na obr.5.28 je znázornený mechanický model tiažovej reťazovky.
Počiatok vzťažného súradnicového systému bol zvolený v najnižšom bode reťazovky, ktorého poloha
zatiaľ nie je známa.
obr.5.28 Mechanický model reťazovky
|
Z hľadiska elastostatiky tiažovej reťazovky treba určiť:
- rovnicu deformovaného tvaru reťazovky y = y(x) a maximálny priehyb
ymax
- veľkosť osovej sily N = N(x) v ľubovolnom mieste xa jej maximálnu
a minimálnu hodnotu
- priebeh normálového (ťahového) napätia a jeho maximálnu a minimálnu hodnotu
- väzbové reakcie v bodoch uchytenia A a B
- celkové predĺženie reťazovky
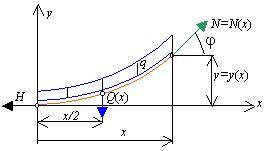
Na obr.5.29 je znázornená vybratá časť reťazovky dvoma myslenými rezmi. Vonkajšie
spojité zaťaženie (napr. vlastná tiaž) musí byť v statickej rovnováhe s vnútornými osovými silami:
H je normálová osová sila v reze v najnižšom bode reťazovky, N(x) je normálová
osová sila (pôsobí v smere dotyčnice k priehybovej čiare) v mieste x. Spojité zaťaženie
q nahradíme výslednicou Q(x) = q.x, pôsobiacou v ťažisku vybratej
časti reťazovky.
obr.5.29 Rovnováha vybratej časti reťazovky
|
Pre vybratú časť reťazovky možno napísať tri statické podmienky rovnováhy:
Z momentovej rovnice rovnováhy k bodu C možno určiť rovnicu priehybovej čiary
reťazovky:
Čo predstavuje rovnicu paraboly. Vlákna, spĺňajúce túto rovnicu nazývame
parabolické reťazovky.
V prípade známej osovej sily H možno z rovnice reťazovky určiť polohu
bodov A,B a prevýšenie h:
Zo silových rovníc vyplýva:
Umocnením a sčítaním týchto dvoch rovníc dostaneme
Je zrejmé, že ak:
Za predpokladu b>a je NB>NA
, a teda NB = Nmax - maximálna osová sila.
Z uvedeného
vyplýva, že minimálna osová sila je v najnižšom bode reťazovky a maximálna osová sila je vo
vyššom závese reťazovky.
Priebeh normálového napätia bude úmerný priebehu osových síl:
Pevnostná podmienka reťazovky má potom tvar
Splnenie tejto podmienky zaručuje dostatočnú pevnosť reťazovky po jej celej
dĺžke. Dovolené napätie je obvykle predpísané normou STN.
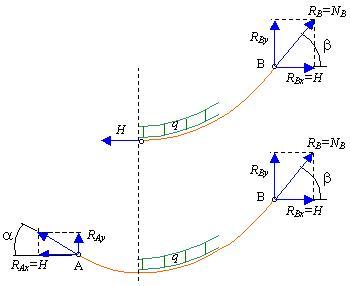
Na obr.5.30 je uvoľnená reťazovka s väzbovými reakciami v bodoch A a B.
obr.5.30 Väzbové reakcie
|
Z podmienky rovnováhy do osi x vyplýva: RBx =
RAx = H
Keďže väzbová reakcia v bode A musí byť v rovnováhe s
osovou silou NA, potom RA = NA, resp. v
bode B je RB = NB
Potom zvislé zložky reakcií sú:
a ďalej
čím je daný sklon priehybovej čiary v závesoch A a B.
Celkové predĺženie reťazovky bude
 s =
s-s0, kde s0 je pôvodná (nedeformovaná) dĺžka
vlákna, a s je nová dĺžka vlákna po jeho predĺžení od vlastnej tiaže. s =
s-s0, kde s0 je pôvodná (nedeformovaná) dĺžka
vlákna, a s je nová dĺžka vlákna po jeho predĺžení od vlastnej tiaže.
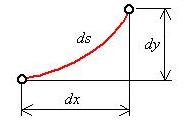
Na obr.5.31 je
znázornená elementárna časť deformovaného vlákna.
obr.5.31 Elementárna časť vlákna
|
Celková dĺžka zaťaženej reťazovky je
Použijúc zjednodušujúce pravidlo (1 + p)a = 1 + p.a
na druhý člen pod odmocninou
potom
pričom l = a + b.
Podobne, celkové predĺženie
Pretože
potom
Pôvodná dĺžka reťazovky je
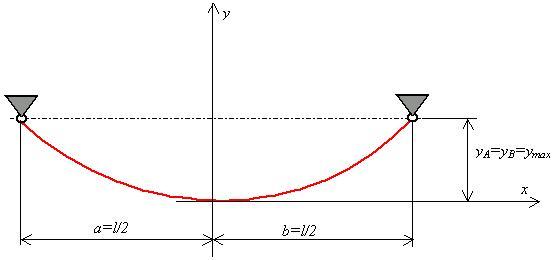
Na obr.5.32 je znázornená symetrická reťazovka (bez prevýšenia úchytných bodov,
t.j. yB - yA = 0).
obr.5.32 Symetrická reťazovka
|
Táto reťazovka je špeciálnym prípadom reťazovky s prevýšením úchytných bodov.
Úpravou predtým odvodených vzťahov dostaneme nasledujúce rovnice symetrickej reťazovky:
a) rovnica priehybovej čiary
b) osová sila
c) pevnostná podmienka
d) deformovaná dĺžka reťazovky
e) celkové predĺženie reťazovky
f) počiatočná dĺžka reťazovky
Poznámka:
Pre prípad, že sú splnené predpoklady
uvedené v úvode k tejto kapitoly, je potrebné použiť presné vzťahy vedúce na rovnicu vlákna typu
kosínusu hyperbolického. Tieto vzťahy možno nájsť v práci: Fecko, Š. - Žiaran, J. - Varga, L.:
Elektrické siete, Edičné stredisko SVŠT, Bratislava 1990.
Riešené príklady reťazovky
Príklad č.1 Symetrická reťazovka
Elektrické lano
AlFe 240/39 má rozpätie l = 300m. Prierezová plocha vodiča je S =
281,6mm2, menovitá hmotnosť vodiča je m = 0,9844 kg/m, čomu odpovedá spojité
zaťaženie q = 9,844 N/m. Modul pružnosti lana je E = 73861 N/mm2,
zaručená ťahová sila je Fp = 76943 N s odpovedajúcou medzou pevnosti
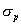 =
Fp/S = 273,23 N/mm2. Dovolené namáhanie v ťahu je =
Fp/S = 273,23 N/mm2. Dovolené namáhanie v ťahu je
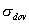 =
51,79 N/mm2. =
51,79 N/mm2.
Treba určiť:
a) Maximálnu osovú silu od spojitého zaťaženia
q: Nmax = ?
b) Minimálnu osovú silu Nmin = H = ?
c) Maximálny priehyb lana yA =
yB =
ymax = ?
d) Pôvodnú nedeformovanú dĺžku lana s0
Riešenie
a) Maximálnu osovú silu vypočítame z pevnostnej podmienky:
Po dosadení je hraničná hodnota ťahovej sily
Nmax = 281,6 . 51,79 = 14584,064 N.
b) Minimálnu ťahovú silu Nmin = H vypočítame zo vzťahu
Riešením je sila H = 14509,12 N
Z
riešenia vyplýva, že ťahová sila sa po dĺžke reťazovky výrazne nemení.
c) Maximálny priehyb reťazovky
d) Pôvodná dĺžka lana
pričom deformovaná dĺžka vodiča s = 300,5178m, a
celkové predĺženie  s = 0,2099m. s = 0,2099m.
a) Staticky určité úlohy namáhania osovou
silou
Úlohy tohto typu možno uvedenými metódami riešiť takto:
- Zostavíme matematický a fyzikálny model riešenej úlohy na prút (tyč) zaťažený osovými
silami.
- Podľa počtu nespojitosti prierezu a zaťaženia prúta si zvolíme príslušný počet úsekov a
v nich myslené rezy.
- Do myslených rezov vložíme výslednicu vnútorných síl
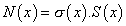 v kladnom zmysle
(von z rezu). v kladnom zmysle
(von z rezu).
- Zo statických podmienok rovnováhy odrezanej časti tyče určíme výslednicu vnútorných síl,
prípadne napätia
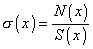 v príslušných rezoch. v príslušných rezoch.
- Nakreslíme priebeh osových síl N(x) a napätia
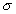 (x) po celej dĺžke
tyče. (x) po celej dĺžke
tyče.
- Určíme nebezpečný prierez a urobíme pevnostný návrh tyče.
- Vypočítame celkové predĺženie tyče.
Priklad 1
Ťahadlo štvorcového prierezu (obr.
5.33a) je namáhané silami F. Určite prierez prúta a jeho celkové predĺženie, keď je
dané : . .
Riešenie
Model ťahadla je znázornený na obr.5.33b. V ďalšom
výpočte zanedbáme oslabenie prierezu ťahadla dierami pre spojovacie kolíky.
Vzhľadom na nespojitosť zaťaženia treba zvoliť dva úseky na tyči (I. a II.) a v nich myslené
rezy. Bod 3. uvedeného postupu je zrejmý z obr.5.33c, d. Z podmienky rovnováhy síl do smeru
osi x pre osovú silu v myslených rezoch x1 a x2
máme:
obr.5.33 Výpočet napätia
|
Priebeh napätia po dĺžke tyče je znázornený na obr.5.33e. Tyč je namáhaná
čistým ťahom. Nebezpečný prierez sa nachádza v mieste maximálneho napätia
teoreticky v ľubovoľnom reze z intervalu ( l/2, l ). Pevnostná
podmienka je
Celkové predĺženie tyče bude rovné súčtu predĺžení jej dvoch úsekov
Z výsledného vzťahu pre  vidieť, že celkové predĺženie je dané tiež súčtom
predĺžení od jednotlivých zaťažujúcich síl. Ak uvážime aj vlastnú tiaž, musíme do ťažísk
jednotlivých odrezaných častí vložiť objemovú silu, ktorá je úmerná objemu odrezanej časti
tyče (obr. 5.28a, b). vidieť, že celkové predĺženie je dané tiež súčtom
predĺžení od jednotlivých zaťažujúcich síl. Ak uvážime aj vlastnú tiaž, musíme do ťažísk
jednotlivých odrezaných častí vložiť objemovú silu, ktorá je úmerná objemu odrezanej časti
tyče (obr. 5.28a, b).
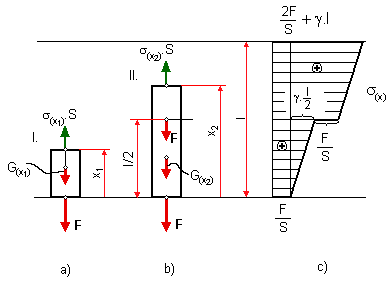
obr.5.34 Zaťaženie vlastnou tiažou
|
Pre úsek I. a II. máme:
Napätie 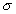 (x1) a (x1) a 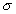 (x2) sú
dané súčtom napätia od zaťažujúcich síl F a vlastnej tiaže (x2) sú
dané súčtom napätia od zaťažujúcich síl F a vlastnej tiaže 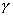 . Ich priebeh je na obr.
5.33c. Nebezpečný prierez je v mieste votknutia, kde . Ich priebeh je na obr.
5.33c. Nebezpečný prierez je v mieste votknutia, kde
Prierez tyče
Pre celkové predĺženie tyče platí:
Z priebehu napätia 5.33e a 5.33c vidieť, že využitie únosnosti prierezu je
efektívne len v nebezpečnom priereze. Ostatné prierezy sú využité nehospodárne. Preto treba
voliť prierez tyče odstupňovaný, prispôsobený veľkosti osových síl v jednotlivých
úsekoch.
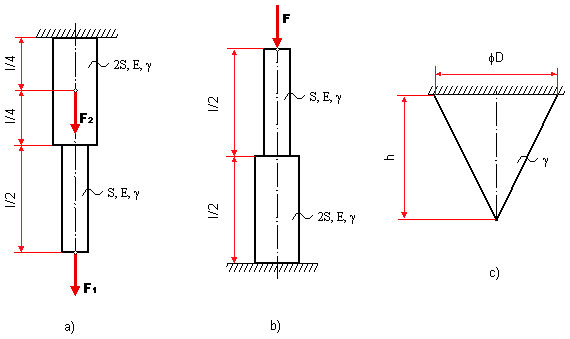
Priklad 2
Riešte úlohy staticky určitého ťahu
(tlaku) podľa obr. 5.35a, b, c. Určite priebeh napätia a celkové predĺženie (skrátenie) tyče.
Z pevnostnej podmienky určite veľkosť nebezpečného prierezu. Úlohy riešte všeobecne postupom zhodným
, aký bol použitý v príklade 1.
obr.5.35 Príklady úloh
|
b) Staticky neurčité úlohy namáhania osovou
silou
Ak nemožno osovú silu určiť zo statických podmienok rovnováhy, úloha je
staticky neurčitá. V tomto prípade treba rovnice rovnováhy doplniť deformačnými
podmienkami.
Postup riešenia
- Úlohu staticky neurčitú nahradíme úlohou staticky určitou, a to tak, že prebytočnú
väzbu odstránime a nahradíme ju staticky neurčitými reakciami.
- Podľa počtu staticky neurčitých reakcií napíšeme príslušný počet deformačných podmienok
(napr. celkové predĺženie alebo skrátenie tyče je nulové) a z nich vypočítame staticky
neurčité reakcie.
- V ďalšom postupujeme ako pri úlohách staticky určitých s tým, že vypočítané staticky
neurčité reakcie považujeme za ďalšie vonkajšie zaťaženie.
Riešenie takýchto úloh je uvedené v časti internetovej učebnice "Príklady".
|

 Výučba
Mechaniky
Výučba
Mechaniky