|
Učebný cieľ kapitoly
Po preštudovaní tejto kapitoly by ste mali ovládať:
- Definíciu a matematické vyjadrenie Hookovho zákona jednoosovej a rovinnej napätosti.
- Obsah Hookovho zákona priestorovej napätosti.
- Ako možno určiť pomernú zmenu objemu.
- Vyjadrenie energie napätosti.
- Vyjadrenie závislosti medzi modulom pružnosti v ťahu (tlaku), šmyku a Poissonovou konštantou.
Vzájomnú závislosť medzi napätím 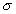 a pomerným predĺžením a pomerným predĺžením 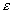 tyče nám vyjadruje Hookov zákon v tvare tyče nám vyjadruje Hookov zákon v tvare
kde E sme nazvali modulom pružnosti materiálu v ťahu. Platnosť Hookovho zákona sa zovšeobecňuje aj pre rovinnú a priestorovú napätosť.
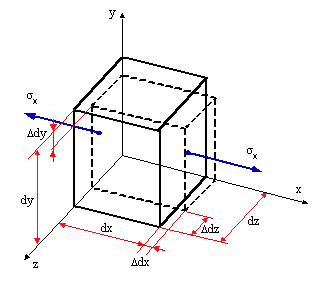
Treba určiť pretvorenie elementárneho hranola, na ktorý pôsobí len napätie 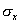 (obr.7.1). (obr.7.1).
obr.7.1 Pretvorenie hranola
|
Pre smer osi x možno napísať Hookov zákon:
Okrem predĺženia 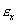 sa hranol priečne zúži o rovnaké pomerné hodnoty (vyplýva to z pozorovania deformácie ťahanej tyče) sa hranol priečne zúži o rovnaké pomerné hodnoty (vyplýva to z pozorovania deformácie ťahanej tyče)
Z toho vyplýva, že aj priamková napätosť vyvoláva priestorové pretvorenie.
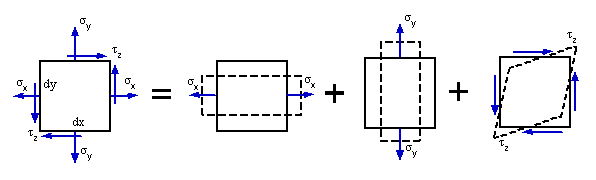
Rovinná napätosť je určená napätiami 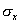 , , 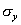 , , 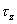 . Na základe zákona o superozícii účinkov budeme vyšetrovať pretvorenie hranola postupne od jednotlivých zložiek napätia (obr. 7.2). . Na základe zákona o superozícii účinkov budeme vyšetrovať pretvorenie hranola postupne od jednotlivých zložiek napätia (obr. 7.2).
obr.7.2 Superpozícia účinkov
|
Vyjdeme z predpokladu, že normálové napätia spôsobia pomerné predĺženie hrán a šmykové napätie spôsobí zmenu pravých uhlov (pomerné skosenie) elementárneho hranola.
Pretvorenie od 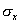 : :
Pretvorenie od 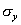 : :
Celkové pomerné predĺženie bude:
Pomerné skosenie od 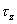 je dané Hookovým zákonom v šmyku je dané Hookovým zákonom v šmyku
Posledné dve rovnice nazývame rovnicami elasticity. Podobne ako pri jednoosovej napätosti, aj pri priamkovej napätosti je pretvorenie priestorové. V špeciálnom prípade, ak 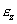 je veľmi malé, možno ho v praktických úlohách zanedbať, a vtedy hovoríme o rovinnej deformácii. je veľmi malé, možno ho v praktických úlohách zanedbať, a vtedy hovoríme o rovinnej deformácii.
Z týchto rovníc možno stanoviť inverznú závislosť
ktorú nazývame zovšeobecneným Hookovým zákonom rovinnej napätosti. Ľahko možno ukázať, že v maticovom zápise bude mať tvar
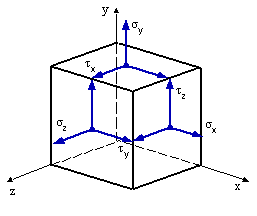
Postupným určením pretvorenia hranola od napätí 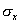 , , 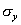 , , 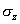 , , 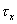 , , 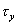 , , 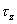 (obr.7.3) a sčítaním jeho zložiek (podobne ako pri rovinnej napätosti) dostaneme: (obr.7.3) a sčítaním jeho zložiek (podobne ako pri rovinnej napätosti) dostaneme:
obr.7.3 Priestorová napätosť
|
Tieto rovnice predstavujú rovnice elasticky priestorovej napätosti. Inverzné vzťahy k nim značia zovšeobecnený Hookov zákon priestorovej napätosti:
Úpravou týchto rovníc možno maticový tvar Hookovho zákona (obvykle sa používa Poissonova konštanta 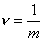 ) )
Uvažujeme elementárny hranol s dĺžkou strán dx, dy a dz. Pretvorenie elementárneho hranola je vo všeobecnosti dané pomernými predĺženiami 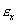 , , 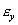 , , 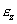 a pomernými skoseniami a pomernými skoseniami 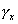 , , 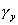 a a 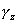 . Pôvodný objem hranola bol . Pôvodný objem hranola bol
Ak zanedbáme vplyv zmeny pravých uhlov hranola na zmenu dĺžok jeho hrán, bude zmena objemu spôsobená predĺžením hrán hranola od pomerných predĺžení
Po roznásobení výrazov v zátvorkách a zanedbaním mocnín veličín malého rádu dostaneme:
z toho zmena objemu
a pomerná zmena objemu
t.j. je rovná súčtu pomerných predĺžení strán hranola. Ak dosadíme do pomernej zmeny objemu rovnice elasticity, dostaneme:
Poznámka: V prípade všestranného ťahu alebo tlaku bude
čo znamená, že
Pre nestlačiteľné telesá je pomerná zmena objemu 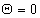 . Potom musí platiť m - 2 = 0 a v tom prípade m = 2 ( . Potom musí platiť m - 2 = 0 a v tom prípade m = 2 (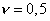 ). ).
Z hľadiska fyzikálneho významu pre rovnice pomernej zmeny objemu musí platiť:
V opačnom prípade, t. j. pre 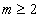 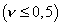 , by bola, ako to vyplýva z hore uvedených rovníc, pri všestrannom ťahu pomerná zmena objemu , by bola, ako to vyplýva z hore uvedených rovníc, pri všestrannom ťahu pomerná zmena objemu 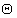 záporná, čo zrejme, odporuje skutočnosti. záporná, čo zrejme, odporuje skutočnosti.
Celková energia napätosti bude daná súčtom energií napätosti od jednotlivých napätí 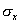 , , 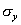 , , 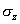 , , 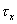 , , 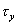 , , 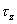
Využitím vzťahov zo 6.kapitoly potom platí:
Merná energia napätosti (ne jednotku objemu) bude
Ak použijeme rovnice elasticity, dostaneme:
Ak je rovinná napätosť zadaná hlavnými napätiami 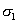 , , 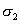 a a 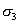 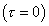 , posledná rovnica prejde do tvaru , posledná rovnica prejde do tvaru
V prípade rovinnej napätosti treba do posledných dvoch vzťahov dosadiť 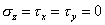 , resp. , resp. 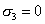 . .
V prípade jednoosovej napätosti je len 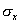 rôzne od nuly, resp. rôzne od nuly, resp. 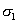 je rôzne od nuly. je rôzne od nuly.
Medzi modulom pružnosti v ťahu - tlaku E, modulom pružnosti v šmyku G a Poissonovou konštantou m existuje závislosť, ktorú môžeme ľahko odvodiť.
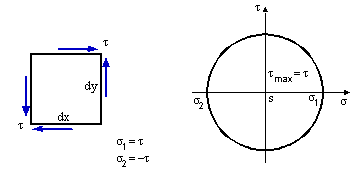
Uvažujme pritom elementárny hranol zaťažený samotnými šmykovými napätiami (obr. 7.4a) ako špeciálny prípad rovinnej napätosti.
obr.7.4 Čistý šmyk
|
Merná energia napätosti prostého šmyku podľa rovnice je
Mernú energiu napätosti prostého šmyku možno však vyjadriť aj ako
kde podľa Mohrovej kružnice napätí (obr.7.4) je 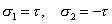 , a ak za tieto hodnoty dosadíme do poslednej rovnice, dostaneme: , a ak za tieto hodnoty dosadíme do poslednej rovnice, dostaneme:
Rovnice pre 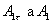 v tomto prípade vyjadrujú mernú energiu napätosti toho istého prípadu, a teda musí byť v tomto prípade vyjadrujú mernú energiu napätosti toho istého prípadu, a teda musí byť
t.j.
a z toho modul pružnosti v šmyku bude
|

 Výučba
Mechaniky
Výučba
Mechaniky