|
Učebný cieľ kapitoly
Po preštudovaní tejto kapitoly by ste mali ovládať:
- Charakteristiku kvadratických momentov prierezových plôch.
- Ako je definovaný kvadraticky moment plochy k osi a k pólu.
- Ako je definovaný deviačný moment plochy k súradnicovým osiam.
- Definíciu Steinerovej vety a jej použitie.
- Čo sú to hlavné (centrálne) momenty zotrvačnosti (kvadratické momenty) prierezovej plochy.
- Čo sú to centrálne osi zotrvačnosti prierezovej plochy.
- Ku ktorým osiam je deviačný moment plochy nulový.
- Ako sa určia kvadratické momenty plochy k natočeným osiam.
- Matematické vyjadrenie kvadratických momentov plôch pre základné typy prierezov (obdĺžnik, štvorec, kruh, medzikruh)
- Ako možno určiť polohu ťažiska plochy prierezu pomocou statických momentov.
Pri riešení základných prípadov namáhania - ohybu a krútenia - narazíme na určité typy plošných integrálov, ktoré nazveme momentovými charakteristikami prierezu. Preto sa nimi budeme teraz zaoberať podrobnejšie.
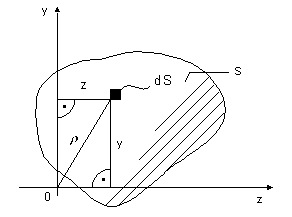
Uvažujeme všeobecný rovinný prierez, ktorého plocha je S (obr.9.1).
obr.9.1 Kvadratické momenty plochy
|
Vybratá elementárna plôška dS je vzdialená o hodnotu 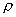 od počiatku vzťažného súradnicového systému. od počiatku vzťažného súradnicového systému.
Moment zotrvačnosti prierezu (kvadratický moment prierezovej plochy) S k osi z, resp. y je definovaný vzťahom
Polárny moment zotrvačnosti (kvadratický moment) plochy S k pólu O je definovaný vzťahom
po dosadení za 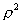 = y2 + z2 bude = y2 + z2 bude
Keďže veličiny z2, y2 a 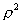 sú vždy kladné, sú aj všetky momenty zotrvačnosti (kvadratické momenty) kladné a majú základný rozmer [m4]. sú vždy kladné, sú aj všetky momenty zotrvačnosti (kvadratické momenty) kladné a majú základný rozmer [m4].
Deviačný moment plochy S je definovaný vzťahom
Z hore uvedenej rovnice vyplýva, že deviačný moment môže byť kladný, záporný alebo nulový. Deviačný moment plochy S k osiam z a y je nulový, ak aspoň jedna z daných osí je osou symetrie prierezu.
Z definície plošných integrálov vyplýva, že ak rozdelíme prierez na niekoľko častí, bude sa celkový moment zotrvačnosti alebo deviačný moment rovnať súčtu príslušných momentov týchto častí, prirodzene, k tým istým osiam. Teda
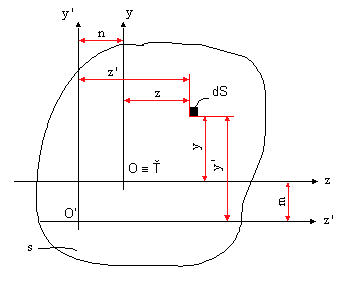
Pomocou Steinerovej vety určíme momentové charakteristiky prierezu k posunutým (rovnobežným) osiam prierezu (obr.9.2).
obr.9.2 Steinerova veta
|
Moment zotrvačnosti napr. k osi z plochy S je definovaný vzťahom
Je zrejmé, že 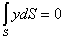 , preto vyjadruje statický moment plochy S k osi predchádzajúcej ťažiskom. , preto vyjadruje statický moment plochy S k osi predchádzajúcej ťažiskom.
Podobne možno určiť moment zotrvačnosti k osi y
Podobne moment k posunutým osiam je
kde
Potom
Hore uvedené rovnice sú matematickým vyjadrením Steinerovej vety, ktorá hovorí:
Momentové charakteristiky prierezu (Iz', Iy', Dz'y') k posunutým osiam sú rovné súčtu momentovej charakteristiky (Iz, Iy, Dzy) k osiam, ktoré prechádzajú ťažiskom prierezu a prírastku, daným súčinom veľkosti plochy prierezu a štvorca posunutia osí (pri deviačnom momente je to súčin obidvoch posunutí osí).
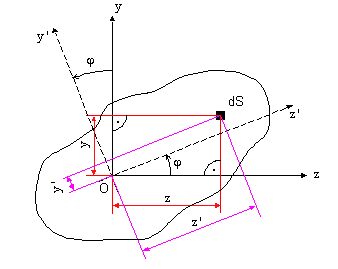
Momenty zotrvačnosti a deviačný moment k natočeným súradniciam z a y sú (obr.9.3)
obr.9.3 Kvadratický moment plochy k natočenej osi
|
Pri transformácii pôvodného súradnicového systému z, y natočením o uhol 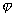 do novej polohy z', y' platí transformačný vzťah do novej polohy z', y' platí transformačný vzťah
Použitím tohoto transformačného vzťahu momenty zotrvačnosti a deviačný moment bude
Uvedené rovnice možno ešte upraviť pomocou vzťahov:
na tvar
Tieto rovnice sú podobné rovniciam pre 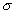 a a 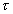 pri rovinnej napätosti. V týchto rovniciach si navzájom zodpovedajú veličiny: pri rovinnej napätosti. V týchto rovniciach si navzájom zodpovedajú veličiny:
Hľadaním extrémnych hodnôt Iz' a Iy', dostaneme hlavné momenty zotrvačnosti
Osi zodpovedajúce hlavným momentom zotrvačnosti nazývame hlavnými osami zotrvačnosti prierezu. Podobne ako pri rovinnej napätosti, môžeme momenty zotrvačnosti a deviačné momenty znázorniť Mohrovou kružnicou v súradniciach I a Dzy. Hlavné momenty zotrvačnosti k osiam, ktoré prechádzajú ťažiskom prierezu, nazývame hlavnými centrálnymi momentmi zotrvačnosti prierezu.
Polomer zotrvačnosti, napr. k osi z je definovaný vzťahom
kde Iz je moment zotrvačnosti plochy S k osi z. Rozmer polomeru zotrvačnosti je dĺžkový a značí takú vzdialenosť od osi z, že plocha S sústredená v tejto vzdialenosti má moment zotrvačnosti Iz = iz2S.
Je teda zrejmé, že najväčšie a najmenšie hodnoty polomeru zotrvačnosti pre osi prechádzajúce jedným bodom budú prislúchať hlavným osiam zotrvačnosti.
Príklad 1
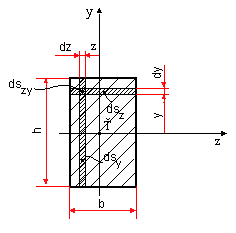
Pre obdĺžnikový prierez so stranami b × h určite hlavné centrálne momenty zotrvačnosti (obr.9.4).
obr.9.4 Obdĺžnikový prierez
|
Riešenie
Hlavné centrálne momenty zotrvačnosti určíme podľa hore uvedených vzťahov. Pretože poloha ťažiska je jednoznačne daná, potrebujeme ešte určiť momenty zotrvačnosti a deviačný moment k dvom navzájom kolmým osiam prechádzajúcim ťažiskom prierezu Iz a Iy.
Podľa definície
Potom centrálne hlavné momenty zotrvačnosti sú:
Z výsledku je zrejmé, že osi z a y sú hlavnými centrálnymi osami zotrvačnosti prierezu.
V prípade štvorcového prierezu b = h = a bude
Príklad 2
Určite momenty zotrvačnosti obdĺžnikového prierezu k osiam z a y, ktoré sú vodorovne posunuté od centrálnych osí zotrvačnosti prierezu o hodnotu 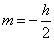 a a 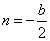 (obr.9.5). (obr.9.5).
obr.9.5 Posunuté osi
|
Riešenie
Momenty zotrvačnosti (kvadratické momenty plochy prierezu) možno určiť priamo z definície alebo pomocou Steinerovej vety. Použitím Steinerovej vedy dostaneme:
Príklad 3
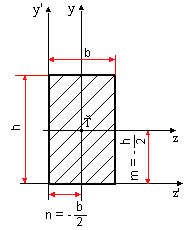
Určite hlavné centrálne momenty zotrvačnosti medzikruhového prierezu podľa obr.9.6.
obr.9.6 Medzikruhový prierez
|
Riešenie
Pre kruhový prierez platí:
Polárny moment zotrvačnosti medzikruhu bude rovný rozdielu polárneho momentu prierezu priemeru D a vybratej kruhovej časti prierezu d
Potom
Je zrejmé, že Iz a Iy sú zároveň hlavnými centrálnymi momentmi zotrvačnosti prierezu. Každá os predchádzajúca ťažiskom medzikruhového prierezu je hlavnou centrálnou osou zotrvačnosti.
V prípade plného prierezu (d = 0) bude
Príklad 4
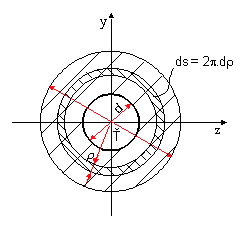
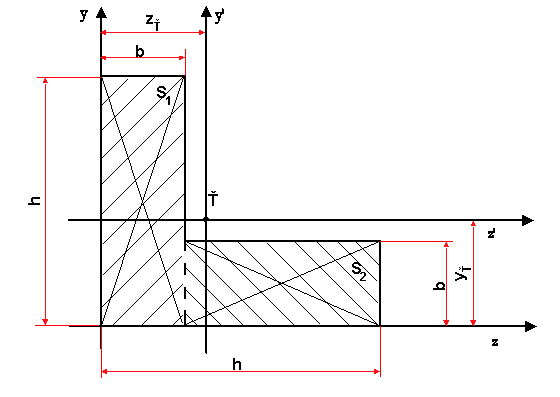
Určite hlavné centrálne momenty zotrvačnosti rovnoramenného L - valcovaného profilu (obr.9.7).
obr.9.7 Zložený profil
|
Riešenie
- Určime polohu ťažiska prierezu.
- Určíme Iz', Iy' a Dz'y' k zvoleným navzájom kolmým osiam z a y, ktoré prechádzajú ťažiskom prierezu.
- Určime hlavné centrálne momenty zotrvačnosti I1, I2.
- Polohu ťažiska prierezu určíme zo statických momentov plochy prierezu ku vhodne zvoleným osiam z a y
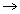 Uz a Uy: Uz a Uy:
pričom Uz1 a Uz2 sú statické momenty plôch S1 = hb a S2 = b(h-b). Vzhľadom na symetriu prierezu je zrejmé, že
-
Moment zotrvačnosti k osi z podľa Steinerovej vety bude (obr.9.8):
obr.9.8 Kvadratické momenty L profilu
|
Tým je Iz' určený. Vzhľadom na symetriu prierezu platí:
Deviačný moment
pretože deviačné momenty plôch S1 a S2 k osiam prechádzajúcim ťažiskami časti prierezu sú rovné nule.
-
Hlavné centrálne momenty sú:
Možno dokázať, že I. centrálna os zotrvačnosti zviera s osou z uhol 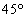 a II. Centrálna os je na ňu kolmá. a II. Centrálna os je na ňu kolmá.
Poznámka: Podobným spôsobom určujeme momentové charakteristiky aj pre iné typy zložených plôch. Pre najčastejšie používané prierezy valcovaných profilov (C, I, L a iné) sú momenty zotrvačnosti prierezov stanovené v strojníckych tabuľkách.
|

 Výučba
Mechaniky
Výučba
Mechaniky