|
Učebný cieľ kapitoly
Prvý zákon termodynamiky - ako aplikácia zákona zachovania energie pre
termodynamické procesy (procesy premeny tepla na prácu) - je obsahom už základného kurzu
fyziky na technických vysokých školách. Táto kapitola je preto čiastočne opakovaním, naviac definuje
ďalšie energetické veličiny, objasňuje ich fyzikálny obsah, rozlišuje aplikácie 1. zákona
termodynamiky pre uzavreté a otvorené sústavy a práce získané v týchto sústavách.
Po preštudovaní tejto kapitoly by mal čitateľ zvládnuť:
- základné energetické veličiny
- prvú vetu termodynamiky pre uzavreté i otvorené sústavy
- základné tepelné diagramy a ich význam v energetike
Termodynamické veličiny delíme na intenzívne a extenzívne.
Intenzívne veličiny sú také, ktoré nezávisia na množstve látky, napr. už uvedené základné stavové veličiny, ako je teplota T, tlak p a iné.
Extenzívne veličiny závisia od množstva látky napr. objem V a
ďalšie, ktoré uvedieme, ak podelíme extenzívnu veličinu množstvom látky m, dostávame z
extenzívnej veličiny intenzívnu, ktorej tiež hovoríme merná veličina
a označujeme ju malými písmenami. Napr. merný objem:
Túto formálnu dohodu zachováme aj v ďalšom texte aby už zo zápisu bolo jasné o akú
veličinu sa jedná.
Teplo Q [J]. Pojmom teplo nemáme
na mysli absolútnu hodnotu, ale teplo odovzdané, resp. získané, t.j. časť vnútornej energie, ktorá sa
vymieňa medzi sústavami alebo ich časťami s rôznymi teplotami.
Práca A [J]. Termodynamický obsah
pojmu práca závisí od termodynamickej zmeny a od spôsobu, akým ju získavame (z uzavretej alebo
otvorenej sústavy), preto pojem práca bude definovaný až s formuláciami 1.zákona termodynamiky pre
otvorené a uzavreté sústavy. V súvislosti s 1.zákonom termodynamiky dokážeme že:
Práca dodaná - konaná je
záporná
získaná - expanzná je kladná
teplo dodané (napr. ohrevom) je kladné
odobrané (napr. chladením) je záporné
Vnútorná energia - U [J] je súčet
potenciálnej a kinetickej energie častíc. Pre ideálny plyn (neexistujú príťažlivé sily medzi
molekulami) je jednoznačne určená kinetickou energiou molekúl, ktorá závisí len od teploty.
Podľa kinetickej teórie plynov je pre 1kg plynu merná vnútorná energia:
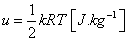
|
(2-1)
|
kde k - je počet stupňov voľnosti molekuly,
R - plynová konštanta,
T - absolútna teplota.
Nulová hodnota vnútornej energie najčastejšie býva definovaná pre teplotu
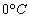 ,
t.j. u0 = 0 pre ,
t.j. u0 = 0 pre
T0 = 273 K. Vo výpočtoch nás však
zaujímajú len zmeny vnútornej energie 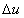 , preto jej absolútna hodnota nemá veľký význam. , preto jej absolútna hodnota nemá veľký význam.
Entalpia - I [J] alebo aj tepelný
obsah je kombinácia už známych stavových veličín. Pre 1 kg látky je:
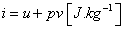
|
(2-2)
|
Je dôležitou stavovou veličinou, vystupujúcou v tepelných bilanciách. Jej fyzikálny
obsah možno objasniť až v súvislosti s matematickou formuláciou 1. zákona termodynamiky.
Entrópia - S [J.K-1].
Umožňuje vyjadriť elementárne dodané teplo dQ, dodávané pri teplote T ako
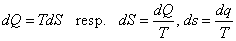
|
(2-3a)
|
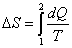
|
(2-3b)
|
Zjednodušuje tepelné bilancie, zakresľovanie termodynamických zmien do diagramov,
posúdenie vplyvu disipácie energie (trenia). Jej význam a podstatu objasníme až v ďaľšom texte,
najmä v súvislosti s 2. zákonom termodynamiky.
Práca A ani teplo Q nie sú stavové
veličiny, pretože ich veľkosť závisí od cesty (termodynamickej zmeny) zo stavu počiatočného
na stav konečný. Vnútorná energia U, entalpia I a entrópia S sú stavové
veličiny. Tieto tvrdenia dokážeme v súvislosti s 1. zákonom termodynamiky.
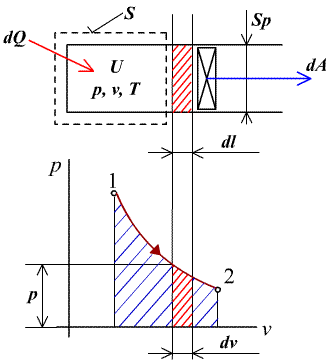
Je vyjadrením zákona zachovania energie pre kvázistatický stav. Plyn v uzavretej sústave, ohraničenej kontrolnou plochou S ( napr. plyn vo valci uzavretom piestom - obr.2.1), má vnútornú energiu U. Pri dodávke tepla dQ zvýši sa jeho teplota o dT (t.j. vnútorná energia o dU), plyn zväčší svoj objem o dV, piest sa posunie o dl a vykoná prácu dA. Zmeny tlaku a objemu sledujeme v pracovnom diagrame p - v. Dodané teplo sa teda využilo na zvýšenie vnútornej energie a na vykonanie vonkajšej práce.
obr.2.1 Premena tepla na prácu v uzavretej sústave
|
Zákon zachovania energie možno písať:
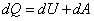
|
(2-4a)
|
a pre 1 kg:
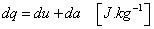
|
(2-4b)
|
Rovnice (2-4) sú matematickou formuláciou 1. zákona termodynamiky. Teraz bližšie
objasníme veličiny v rovniciach (2-4).
Práca - je súčin sily na piest a dráhy piesta:
kde
teda
resp.pre 1 kg
a pre konečnú zmenu od stavu 1 do stavu 2:
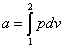
|
(2-5c)
|
rovnicu (2-4b) možno potom písať v tvare:
Z pracovného diagramu p-v vidieť, že práca má
geometrický význam plochy, vymedzenej krivkou termodynamickej zmeny a jej priemetom na os v.
Táto práca s nazýva práca objemová alebo
absolútna. Získavame ju pri zmenách, uskutočnených
jednorázovo (bez opakovania). Je zrejmé, že pre opakovanie zmeny 1-2
podľa obr.2.1 musíme piest vrátiť do východiskovej polohy 1, t.j. uskutočniť 2-1, na čo musíme
dodať prácu, resp. plyn ochladiť, takže výsledný efekt, vonkajšia získaná práca po uskutočnení
cyklu 1-2, 2-1 nebude rovná absolútnej práci, získanej pri 1-2. Napr. pre uskutočnenie pracovnej
expanzie v spaľovacom motore musíme realizovať aj ďalšie zmeny (výfuk, sanie, kompresia). Vonkajšia
práca je potom daná súčtom kladných a záporných absolútnych prác, získaných, resp. dodaných pri
čiastkových zmenách, ktoré realizujú cyklus.
Poznámka: Prácu prúdových strojov (turbína,
turbokompresor, ventilátor, odstredivé čerpadlo a pod.), ktoré termodynamickú zmenu uskutočňujú
kontinuálne, nemožno počítať podľa vzťahu (2-5c), platného pre uzavreté sústavy. Prúdové stroje
tvoria otvorenú sústavu (hranicou prechádza aj látka), v ktorej vychádza pre prácu vzťah odlišný
od (2-5c) - pozri ďalej.
Vnútorná energia je daná vzťahom (2-1), ale možno
ju vyjadriť aj z predpokladu izochorického deja t.j. v = const. Dosaďme
túto podmienku do rovnice (2-6).Dostávame:
|
da = pdv = 0
|
|
|
(dq)v=k = du
|
(2-7)
|
t.j. dodané teplo pri izochorickej zmene sa premení len na
prírastok vnútornej energie. Ak v = const, možno vyjadriť dodané teplo pomocou mernej
tepelnej kapacity cv a prírastku teploty dT.
|
(dq)v=k = du = cvdT
|
(2-8a)
|
resp.
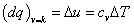
|
(2-8b)
|
za predpokladu, že cv = const, t.j. pre ideálny plyn.
 u
je násobkom u
je násobkom  T, preto je vnútorná energia, rovnako ako teplota
stavovou veličinou. Ľavá časť rovnice
((dq)v=k = du) platí len pre deje izochorické, pravá časť
rovnice (du = cvdT) platí všeobecne, pre ľubovoľné deje.
T, preto je vnútorná energia, rovnako ako teplota
stavovou veličinou. Ľavá časť rovnice
((dq)v=k = du) platí len pre deje izochorické, pravá časť
rovnice (du = cvdT) platí všeobecne, pre ľubovoľné deje.
Entalpia (tepelný obsah) - fyzikálny význam
Derivujeme rovnicu pre entalpiu (2.2.) i = u + pv:
Prvé dva členy na pravej strane sú rovné dq, teda:

|
(2-9)
|
Predpokladajme izobarickú zmenu, t.j. p = const.
Dodané teplo pri izobarickej zmene sa premení na prírastok entalpie. Analogicky ako
v rovnici (2.8a) možno písať:
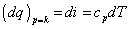
|
(2-10a)
|
resp.
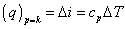
|
(2-10b)
|
za predpokladu, že ide o ideálny plyn, t.j. cp = const.
 i
je násobkom i
je násobkom  T, preto je entalpia, rovnako ako teplota stavovou veličinou. Ľavá časť rovnice
((dq)p=k = di) platí len pre izobarické deje, pravá časť
rovnice (di = cpdT) platí všeobecne, pre ľubovolné deje.
Nulová hodnota entalpie je definovaná pre teplotu
T, preto je entalpia, rovnako ako teplota stavovou veličinou. Ľavá časť rovnice
((dq)p=k = di) platí len pre izobarické deje, pravá časť
rovnice (di = cpdT) platí všeobecne, pre ľubovolné deje.
Nulová hodnota entalpie je definovaná pre teplotu
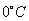 : :
|
i0 = 0 pre T0 = 273 K
|
(2-11)
|
Podľa (2-10b) je entalpia pri ľubovolnej teplote:
|
i - i0 = cp(T - T0) =
cp(t - t0)
|
a s rešpektovaním definície (2-11) je:
Z uvedeného vyplýva, že entalpia má význam tepelného obsahu,
t.j. množstva tepla, potrebného na zohriatie 1kg látky z teploty 0°C na danú teplotu t, ak
zohrievanie prebieha za konštantného tlaku.
Príklady
1. Merná tepelná kapacita vody je
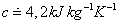 .
Potom entalpia podľa (2-12) bude pri teplote: .
Potom entalpia podľa (2-12) bude pri teplote:
- t = 10°C: i = 4,2.10 = 42 kJ kg-1, čo je
množstvo tepla, potrebné na zohriatie 1 kg vody z 0°C na 10°C, alebo inými
slovami: teplo, ktoré 1 kg vody pri teplote 10°C obsahuje.
- t = 100°C: i = 420 kJ kg-1
- Entaplia pary, ktorá vznikla odparením vody z príkladu b.) pri tlaku 0,1 MPa a
nestačila sa ešte prehriať, t.j. má teplotu 100°C, skladá sa z tepla, potrebného na
dosiahnutie teploty bodu varu a tepla výparného pri danom tlaku. Z tabuliek alebo diagramu
zistíme, že táto entalpia je 2680 kJ kg-1. Teplota sa v priebehu zmeny skupenstva nezmenila, ale entalpia vzrástla. Rovnica (2-12) v oblasti zmeny skúpenstva neplatí, ostáva však v platnosti fyzikálna definícia entalpie ako tepelného obsahu.
2. Z tabuliek alebo diagramu zistíme, že entalpia pary pri parametroch, napr. p = 4 MPa, t = 400°C, je i = 3220 kJ kg -1. To znamená, že potrebujeme 3220 kJ na zohriatie 1 kg vody z teploty
0° C na teplotu bodu varu (pri p = 4 MPa), odparenie a prehriatie na teplotu
400° C, všetko pri tlaku 4 MPa.
Uvedené príklady naznačujú význam entalpie pri tepelných bilanciách.
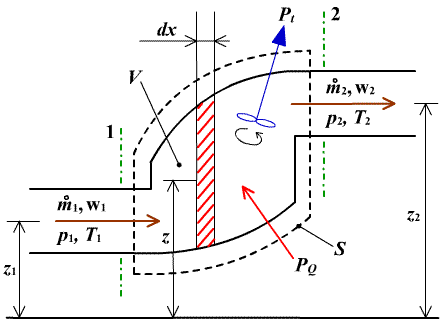
Tento zákon, zvaný tiež zákon o energii, sa odvodí zo zákona o zachovaní energie pre otvorenú sústavu na obr.2.2, ktorý je principiálnou bilančnou schémou činnosti prúdových strojov. Predstavuje kanál, ohraničený kontrolnou plochou S0, ktorého hranicou preteká aj tekutina. Tekutine, uzavretej v kontrolnej ploche S0 s objemom V privádzame zvonka tepelný výkon PQ.
obr.2.2 Premena tepla na prácu v otvorenej sústave
|
Do okolia odovzdávame kontinuálne technický výkon Pt. Hmotnostný prírastok tekutiny 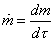 [kg s-1] nesie sebou mernú vnútornú energiu u, mernú potenciálnu energiu ep = gz a mernú kinetickú energiu [kg s-1] nesie sebou mernú vnútornú energiu u, mernú potenciálnu energiu ep = gz a mernú kinetickú energiu 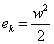 . V objeme V vyjmeme elementárny objem dV, do ktorého dodávame elementárny tepelný výkon dPq a odoberáme elementárny technický výkon dPt. . V objeme V vyjmeme elementárny objem dV, do ktorého dodávame elementárny tepelný výkon dPq a odoberáme elementárny technický výkon dPt.
Bilancia výkonov dáva rovnicu:
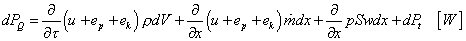
|
(2-13)
|
t.j. dodaný tepelný výkon do elementárneho objemu dV (ľavá strana rovnice) sa premení na :
- zvýšenie celkovej energie za jednotku času (1. člen pravej strany),
- zmenu celkovej energie na úseku dx, t.j. zmenu energie prúdiacej tekutiny medzi vstupným a výstupným prierezom objemu dV (2. člen pravej strany),
- výkon tlakových síl, t.j. výkon potrebný na pretláčanie tekutiny objemom dV, čiže výkon na prekonanie hydraulických strát trením (3. člen pravej strany),
- vonkajší - odoberaný technický výkon (4. člen pravej strany).
Všetky veličiny sú strednými veličinami po priereze. Pre ďalšie úpravy využijeme z mechaniky tekutín rovnicu pre hmotný prietok:
a rovnicu kontinuity v diferenciálnom tvare:
resp.
Ďalej dosadíme z rovnice (2-2) za vnútornú energiu:
za dV = Sdx a vydelíme rovnicu (2-13) dx. Po úprave
dostávame:
Za predpokladu, že:
môžeme derivovať prvé dva členy na pravej strane takto:
Na základe rovnice kontinuity môžeme zrušiť 2. a 4. člen pravej strany a dostaneme po dosadení za ep = gz a ek = w2 / 2 konečný tvar diferenciálnej rovnice energie:
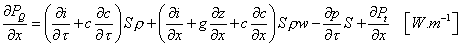
|
(2-14)
|
kde 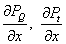 je dodaný, resp. získaný výkon z jednotky dĺžky pre zvolený element. je dodaný, resp. získaný výkon z jednotky dĺžky pre zvolený element.
Pre stacionárne deje sú parciálne derivácie podľa času nulové, rovnica (2-14) sa zjednoduší:
Po integrácii s prihliadnutím na to, že prietoky 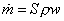 sú na vstupe a výstupe
rovnaké dostávame: sú na vstupe a výstupe
rovnaké dostávame:
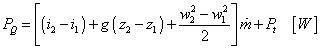
|
(2-15)
|
a po vydelení 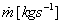 dostávame z dodaných výkonov energie, dodané 1 kg tekutiny: dostávame z dodaných výkonov energie, dodané 1 kg tekutiny:
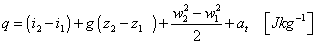
|
(2-16a)
|
V diferenciálnom tvare rovnica bude:
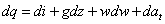
|
(2-16b)
|
Dôležitou vlastnosťou rovníc (2-15) a (2-16) je, že v nich nevystupujú žiadne výrazy, popisujúce mechanizmus procesov medzi vstupným a výstupným prierezom, bilancia práce a tepla závisí len od vstupných a výstupných veličín. Rovnice platia aj pre sústavy s trením, ktorého účinok sa prejaví na výstupných stavových veličinách (vplyv trenia bol rešpektovaný vo východiskovej rovnici (2-13) 3.členom pravej strany).
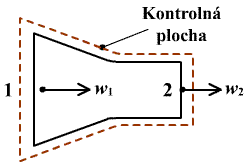
V špeciálnych prípadoch možno rovnicu (2-16b) ďalej zjednodušovať. Pri prúdení plynov a pár dýzou (obr.2.3)
obr.2.3 Prúdenie dýzou
|
možno zanedbať zmenu potenciálnej energie dep = 0 zvyčajne sa neprivádza ani teplo ani práca 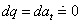 , potom z rovníc (2.16.b) zostáva len , potom z rovníc (2.16.b) zostáva len
Touto tématikou sa zaoberať nebudeme. Zameriame sa však na bilancie tepelných motorov (obr.2.4). V týchto prípadoch možno zanedbať zmenu potenciálnej a kinetickej energie 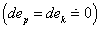 .
Potom dostávame z rovnice (2.16.b) .
Potom dostávame z rovnice (2.16.b)
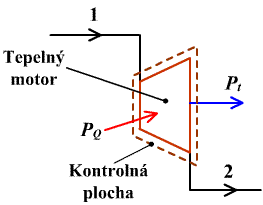
obr.2.4 Bilančná schéma tepelného motora
|
|
dq = di + dat [Jkg-1]
|
(2-18a)
|
Po integrácii od vstupu "1" k výstupu "2" je
a po vynásobení hmotným prietokom 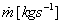
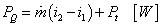
|
(2-18c)
|
kde zrejme sme označili 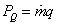 ; ; 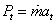
V rovnici (2-18a) vystupuje tzv. technická práca získaná premenou tepelnej energie v otvorených sústavách, t.j. v tepelných motoroch, ktoré uskutočňujú termodynamické zmeny kontinuálne, ako napr. turbíny, turbokompresory, ventilátory a pod. Rovnica (2-18b) je ich najdôležitejšou bilančnou rovnicou.
Technická práca z (2-18b) bude:
kde q je dodané teplo, (i2 - i1) rozdiel entalpií na vstupe a výstupe z motora. Častá je bilancia tepelne izolovanej termodynamickej zmeny (napr. expanzia pary v dokonale izolovanej parnej turbíne). Túto zmenu, nazývanú adiabatická (podrobnejšie v kapitole Základné termodynamické zmeny), charakterizuje podmienka, že teplo zvonka neprivádzame ani neodvádzame, teda teplo pri zmene je konštantné, teda dq = 0!
Potom z rovnice (2-18a) zostáva:
a po integrácií zo stavu 1 (vstup) do stavu 2 (výstup) je
Technickú prácu môžeme okrem rovnice (2-18b) vypočítať aj zo známeho priebehu termodynamickej zmeny, ktorá sa kontinuálne uskutočňuje v tepelnom motore.
Porovnaním rovníc (2-9) a (2-18a):
|
dq = di - vdp
|
|
dq = di + dat
|
zisťujeme že platí:
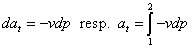
|
(2-20)
|
a technická tlaková práca má, podobne ako práca absolútna, geometrický význam plochy, vymedzenej krivkou termodynamickej zmeny a jej priemetom na os p.
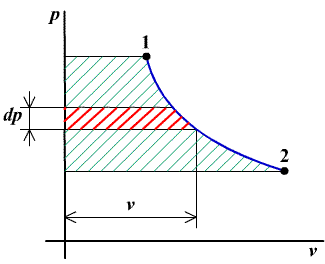
obr.2.5 Geometrický význam technickej práce
|
Z geometrického významu práce na obr.2.5. vyplýva, že veľkosť práce (plochy) závisí od tvaru krivky medzi stavmi 1-2, t.j. závisí od termodynamickej zmeny. Práca, rovnako ako teplo, nie je preto stavová veličina. Na záver tejto kapitoli uveďme ešte rovnicu energie pre nestacionárne procesy v integrálnom tvare. Získame ju integráciou rovnice (2.14) pre konečný objem V, obsahujúci tekutinu s hmotnosťou M. Pri zanedbaní zmeny potenciálnej a kinetickej energie je
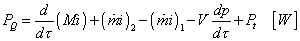
|
(2-21)
|
kde index "2" - výstup, "1" - vstup.
Stavové zmeny látok je niekedy výhodné znázorňovať v rôznych druhoch diagramov. Ich výhodou je názornosť a prehľadnosť a často umožňujú rýchlejšie zistenie potrebných hodnôt. Z celej rady diagramov v rôznych súradnicových systémoch uvedieme len tie, ktoré sú pre naše účely najdôležitejšie.
- p - v diagram
Diagram závislosti merného tlaku od merného objemu. Tento diagram sme už použili pri analýze 1. zákona termodynamiky pre uzavreté a otvorené sústavy. Zahrňme teda len poznatky z tejto analýzy, vzťahujúce sa na p - v diagram.
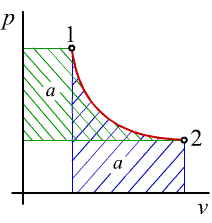
obr.2.6 Geometrický význam absolútnej objemovej a technickej - tlakovej práce
|
Podľa vzťahu (2-5c) je absolútna - objemová práca daná:
a technická - tlaková práca zo vzťahu (2-19):
a význam diagramu je zrejmý z obr.2.6
Zo vzťahov pre prácu (2-5c) a (2-20) vyplýva, že:
expanzná práca - získaná (dv > 0, resp dp < 0) je kladná
kompresná práca - dodaná (dv < 0, resp dp > 0) je záporná
- T - s diagram
vyjadruje závislosť teploty od mernej entrópie
(obr.2.7)
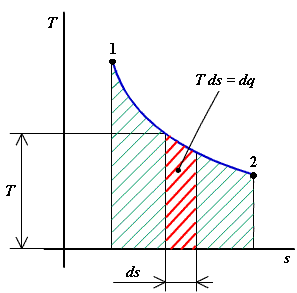
obr.2.7 T - s diagram
|
Pretože platí podľa rovnice (2-3) dQ = TdS, resp. dq = Tds je zrejmé, že geometrický význam plochy pod krivkou termodynamickej zmeny v T - s diagrame je teplo pri zmene dodané alebo odobrané. Teplo dodané (ds > 0) je kladné, teplo odobrané (ds < 0) je záporné.
-
i - s diagram
vyjadruje závislosť mernej entalpie od mernej entrópie (obr.2.8. a,b)
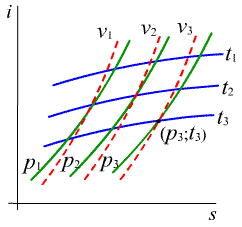
obr.2.8a i - s diagram
|
|
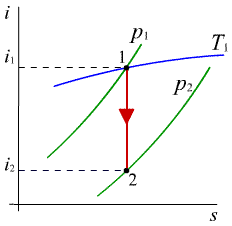
obr.2.8b i - s diagram
|
|
Priebeh izobar a izochor na obr.2.8a je podobný ako u T - s diagramu. K nim pribudli v i - s diagrame naviac izotermy, pretože stav je zvyčajne zadaný tlakom a teplotou a leží na priesečníku danej izobary a izotermy , napr. (p3, t3). K danému stavu ľahko odčítame na stupnici i - entalpiu. Podľa zjednodušenej rovnice 1. zákona termodynamiky pre tepelné motory (2-18a) a pre tepelne izolovanú zmenu (dq = 0) je tecnická práca podľa (2-19b) at = i1 - i2 a zmena (v diagrame p - v vo všeobecnosti hyperbola) sa ľahko znázorní ako čiara s = konšt. Význam i - s diagramu je teda vtom, že
- ľahko nájdeme zadané stavy a im odpovedajúce hodnoty i, potrebné pre tepelné bilancie
- ľahko znázorníme často sa vyskytujúcu adiabatickú zmenu ako čiaru konštantnej entrópie.
|

 Výučba
Termomechaniky
Výučba
Termomechaniky